Внутренняя энергия реального газа.

Взаимодействие между молекулами реального газа обуславливает их взаимную потенциальную энергию , которая переходит во внутреннюю энергию газа наряду с кинетической энергией движения молекул .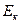

Найдем энергию ван-дер-ваальсовского газа.

Внутренняя энергия такого газа , где

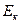— суммарная кинетическая энергия молекул в Ц-системе (связанной с сосудом),

— суммарная энергия взаимодействий молекул (собственная потенциальная энергия).

Найдем .: Работа сил притяжения равна убыли внутренней энергии .

Силы притяжения характеризуются внутренним давлением в уравнении Ван-дер-Ваальса.

Тогда элементарная работа этих сил , где знак минус обусловлен тем, что при расширении газа ( >0) работа должна быть отрицательной, < 0.

Итак, .

Мы представили как убыль некоторой величины — она и является энергией = .

При .

Суммарная же кинетическая энергия 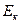зависит от поступательного и внутреннего движений молекул, и определяется как .

Таким образом, внутренняя энергия моля ван-дер-ваальсовского газа

где .

Если газ расширяется в пустоту без теплообмена с окружающими телами, то А = U, Q = 0, и согласно первому началу в этом процессе U= сопst. Значит, с ростом объема температура газа уменьшается (в отличие от идеального газа).

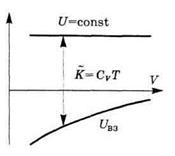Это можно представить и наглядно (рис. 6.6).

Видно, что при расширении газа (увеличении объема V) в случае U=const суммарная кинетическая энергия молекул газа, а значит и температура T, уменьшается. Газ охлаждается.

Теперь получим то же выражение для внутренней энергии, исходя из того, что внутренняя энергия является термодинамическим потенциалом

Из уравнения состояния ван-дер-ваальсовского газа следует, что .

Отсюда .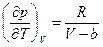

Подставив это выражение, получим .

Произведя интегрирование по V, найдем, что .

Вид функции f (Т) можно установить, воспользовавшись тем, при выражение для внутренней энергии ван-дер-ваальсовского газа должно переходить в выражение для внутренней энергии идеального газа

U = T.

В итоге мы приходим к выражению которое было получено, исходя из других соображений.

Получим для моля ван-дер-ваальсовского газа этого газа уравнение адиабаты в переменных T, V, если известна его молярная теплоемкость .

Согласно первому началу термодинамики

.

Отсюда

Интегрируя это уравнение, получаем ,

Или .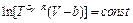

Таким образом, уравнение адиабаты имеет вид .

---

Дата добавления: 2015-08-21