При прочих равных условиях расстояние r1 тем меньше, чем выше температура газа

зависимость W_n от r в области положительных значений Wn настолько «крутая», что даже значительные изменения температуры газа приводят к сравнительно небольшим изменениям величины r1. Поэтому в первом приближении можно считать, что r, зависит только от химической природы газа и представляет собой не что иное, как эффективный диаметр d молекул.

Из сказанного ясно, что возможность представления молекул газа в виде твердых шариков диаметра d связана с очень быстрым увеличением сил взаимного отталкивания молекул реального газа при уменьшении расстояния между ними.

Зависимость взаимной потенциальной энергии W_n двух молекул реального газа от расстояния г между ними неплохо описывается формулой Ленарда-Джонса (1924):

(6.6)

где а₁ и а₂— постоянные положительные коэффициенты, зависящие от химической природы газа.

Дифференцируя выражение(6.6) по r, находим зависимость от r проекции Fr результирующей силы F взаимодействия двух молекул реального газа:

, (6.7)

где и

Анализ формулы:

Первый член в правой части формулы (6.7) соответствует силам межмолекулярного притяжения, которые часто называют ван-дер-ваальсовыми силами по имени нидерландского физика Я. Д. Ван-дер-Ваальса, который впервые начал учитывать межмолекулярное взаимодействие в газах.

Различают три типа сил межмолекулярного притяжения:

· Ориентационные - между полярными молекулами

· индукционные — между полярной и неполярной молекулами

· дисперсионные — между неполярными молекулами, а также между любыми другими парами молекул.

Все они имеют электрическую природу и зависят от расстояния r между молекулами по закону const/r⁷.,,

Второй член в правой части формулы (6.7) соответствует силам взаимного отталкивания молекул. Эти силы обратно пропорциональны r¹³, т. е. играют определяющую роль на малых расстояниях, соответствующих перекрытию электронных оболочек молекул. Существование сил взаимного отталкивания молекул при их очень сильном сближении удалось объяснить только в квантовой механике, основываясь на квантовом принципе запрета Паули.

6.2. Газ Ван-дер-Ваальса

Модели идеального газа, подчиняющегося уравнению Менделеева – Клапейрона .

Однако с ростом давления при постоянной температуре оказывается, что .

При р = 1000 атм. величина становится вдвое больше, чем предписывает модель идеального газа (газ не «сжимается»).

Причин этому две:

1) собственный размер молекул; он и уменьшает объем, доступный для движения молекул, при нормальных условиях он составляет ~0,07 % объема сосуда с газом, а при 100 атм. уже ~70%;

2) сложный характер взаимодействия между молекулами.

Эти причины можно учесть путем введения поправок в уравнение состояния идеальных газов, что и сделал Ван-дер-Ваальс.

B первом приближении молекулы реального газа можно уподобить абсолютно твердым шарикам с диаметром d, между которыми действуют только силы взаимного притяжения. Учитывая конечные размеры молекул, мы приближенно принимаем во внимание действие сил взаимного отталкивания между ними. Такая модель газа, принятая Ван-дер-Ваальсом, позволила ему получить уравнение состояния реального газа более совершенное, чем уравнение Клапейрона — Менделеева.

1. Поправка b.

- связана с собственным объемом молекул,

- ее размерность м /моль.

Каждая молекула реального газа имеет объем .

Поэтому молекулы газа движутся в сосуде менее свободно, чем «точечные» молекулы идеального газа.

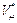Ван-дер-Ваальс учел собственный объем молекул газа путем замены в уравнении Клапейрона — Менделеева полного объема сосуда, занимаемого молем газа, на «свободный» объем:

, (6.8)

где b — поправка Ван-дер-Ваальса, зависящая от собственного объема молекулы – определяет ту часть объема, которая недоступна для движения молекул вследствие их конечных размеров.

Дата добавления: 2015-08-21