Матрицы. Типы матриц.

Если число строк матрицы равно числу столбцов, то матрица называется квадратной.

Если все элементы матрицы равны нулю, то матрица называется нулевой

Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной.

Квадратная матрица называется верхней треугольной (нижней треугольной), если все ее элементы, стоящие ниже (выше) главной диагонали, равны нулю.

Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны 1. Для обозначения единичной матрицы обычно используется буква .

Элементарными преобразованиями матрицы называют:

1) умножение какой-нибудь строки (столбца) на отличное от нуля число;

2) прибавление к какой-нибудь строке (столбцу) другой ее строки (столбца), умноженной на произвольное число;

3) перестановку местами любых двух строк (столбцов).

Линейные операции над матрицами:

Равенство матриц
Матрицы A = || a_{i j} || и B = || a_{i j} || считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны.

Умножение матрицы на число
При умножении матрицы A на число λ (слева или справа) каждый ее матричный элемент умножается на это число

Сложение матриц
Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц A = || a_{i j} || и B = || b_{i j} || является матрица C = || c_{i j} ||, элементы которой равны сумме соответствующих матричных элементов

Умножение матриц: Формула: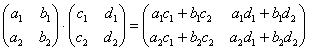

Транспонирование матрицы. Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Обратную матрицу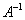можно найти по следующей формуле:

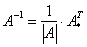, где 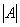– определитель матрицы 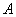, – транспонированная матрица

Ранг матрицы - наивысший порядок отличных от нуля ее миноров.

Дата добавления: 2015-09-03