Определенный интеграл: Если функция является первообразной для на отрезке , то число равное разности называется определённым интегралом от функции на отрезке и обозначается

Свойства определённого интеграла

Свойство 1. Производная от определённого интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела. То есть

Свойство 2. Определённый интеграл от суммы функций равен сумме неопределённых интегралов

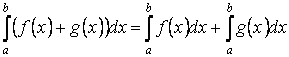
Свойство 3. Постоянный множитель можно выносить за знак определённого интеграла

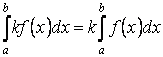
Свойство 4. Если на отрезке , где , функции и удовлетворяют условию , то

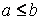Свойство 5. Если и - наименьшее и наибольшее значения функции на отрезке и , то

Свойство 6. Если поменять местами верхний и нижний пределы интегрирования, то определённый интеграл изменит знак

Свойство 7. Для любых трёх чисел справедливо равенство

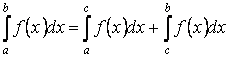
если только все три интеграла существуют.
Свойство 8 (Теорема о среднем). Если функция непрерывна на отрезке , то на этом 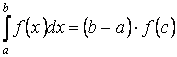отрезке найдётся такая точка , что справедливо равенство:

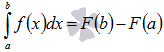
Дата добавления: 2015-09-03