
Читайте также:
|
Две системы линейных уравнений от одного набора x1,..., xn неизвестных и соответственно из m и p уравнений
называются эквивалентными, если их множества решений совпадают
Теорема Кронекера–Капелли (критерий совместности системы линейных уравнений). Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы, т.е. 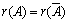 . Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений.
. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений.
Метод Гаусса — Жордана используется для решения систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы.
1. Выбирается первая колонка слева, в которой есть хоть одно отличное от нуля значение.
2. Если самое верхнее число в этой колонке есть нуль, то меняется вся первая строка матрицы с другой строкой матрицы, где в этой колонке нет нуля.
3. Все элементы первой строки делятся на верхний элемент выбранной колонки.
4. Из оставшихся строк вычитается первая строка, умноженная на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) нуль.
5. Далее проводим такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.
6. После повторения этой процедуры n-1 раз получаем верхнюю треугольную матрицу
7. Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.
8. Повторяем предыдущий шаг для последующих строк. В итоге получаем единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).
Решение системы линейных алгебраических уравнений по матричному методу определяется равенством 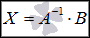 . СИСТЕМУ n ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
. СИСТЕМУ n ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
Пределы: Если число 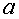 есть предел переменной величины х, то говорят, что х стремится к пределу
есть предел переменной величины х, то говорят, что х стремится к пределу 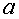
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Первый замечательный предел равен 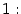
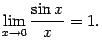
Вторым замечательным пределом называется предел

Свойства бесконечно малых.
1. Если функции 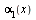 и
и 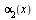 являются бесконечно малыми, то функция
являются бесконечно малыми, то функция 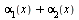 также есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.
также есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.
2. Произведение ограниченной при 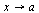 функции на бесконечно малую есть функция бесконечно малая.
функции на бесконечно малую есть функция бесконечно малая.
3. Произведение постоянной на бесконечно малую есть бесконечно малая.
4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое конечное число бесконечно малых.
Дата добавления: 2015-09-03; просмотров: 101 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Матрицы. Типы матриц. | | | Производная |