|
Читайте также: |
Уравнения Максвелла не вытекают из каких-либо более общих теоретических положений, а являются обобщением опыта. При построении теорем за основные принимаются уравнения (3-6), а все остальные законы электродинамики, включая и законы сохранения заряда, получаются как их следствия.
Уравнения Максвелла лежат в основе всей электротехники и радиотехники с её многочисленными разветвлениями (телевидение, радиолокация и прочее). В известной степени они являются фундаментальными уравнениями классической оптики. Так, например, все законы распространения света (переменного электромагнитного поля) могут быть получены из уравнений Максвелла. Наряду с уравнениями Ньютона и законом всемирного тяготения они являются фундаментальными уравнениями классической физики.
Уравнения Максвелла связывают друг с другом пространственные и временные производные напряжённостей и. Это означает, что меняющийся во времени электромагнитный процесс, возникший в некоторый момент в данном месте, вызовет изменение в другом месте с запаздыванием, т.е. утверждается конечная скорость передачи электромагнитных взаимодействий, которая равна:
(в вакууме)
Теория Максвелла имеет границы применения (как и всякая физическая теория). Она применима:
а) для расстояний R между зарядами, превышающих внутриатомные расстояния;
б) для частот изменения поля, не более (это ограничение связано с проявлением на высоких частотах квантовых свойств излучения);
в) для полей, напряжённость которых менее (это ограничение связано с тем, чтобы энергия, получаемая заряженными частицами, была меньше по сравнению со средней энергией беспорядочного движения частиц среды. В вакууме эти ограничения отпадают).
Основные уравнения и законы[править | править вики-текст]
Современная теория магнетизма базируется на следующих основных уравнениях и законах:
Магнитные явления в материальных средах[править | править вики-текст]
Постоянное магнитное поле в веществах [править | править вики-текст]
Микроскопические уравнения [править | править вики-текст]
На микроскопическом уровне электромагнитные поля задаются уравнениями Лоренца — Максвелла (так называемые, микроскопические уравнения). Магнитное поле с микроскопической напряженностью h описывается системой из двух уравнений (СГС):
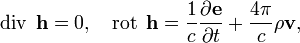
где e — микроскопическая напряжённость электрического поля, а произведение плотности электрических зарядов на их скорость 
соответствует плотности тока. Микроскопические поля являются истинными, то есть возбуждаемыми движением элементарных зарядов в атомах и оно сильно зависит от координат. Здесь ток ассоциируется с орбитальным и спиновым движением внутри атомов (молекулярные токи, концепцию которых предложилАмпер[27]). Переход к макроскопическим уравнениям происходит путём усреднения уравнений Лоренца — Максвелла. При этом среднюю напряжённость микроскопического магнитного поля называют магнитной индукцией[28][29][Комм 3]:
Токи намагничивания и элементарные магнитные моменты [править | править вики-текст]
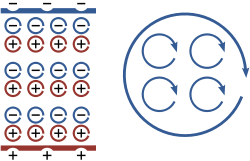
Слева: элементарные электрические диполи, создающие суммарный электрический дипольный момент тела.
Справа: магнитные диполи, являющиеся причиной ненулевой намагниченности тела.
Усреднённые по объему молекулярные токи называют токами намагничивания. Когда внешнего поля нет, токи намагничивания в среднем равны нулю, а воздействие внешнего магнитного поля на вещество связано с их появлением. Если бы они были известны, то для вычисления полей было бы достаточно уравнений Максвелла для вакуума. Молекулярные токи можно интерпретировать как круговые токи, циркулирующие в атомах или молекулах вещества.[30]
С каждым контуром молекулярного тока плотностью j m можно связать магнитный момент p. Это позволяет рассматривать ненамагниченное вещество как такое, где все магнитные моменты отдельных атомов направлены хаотически, а во внешнем магнитном поле они ориентируются определённым образом, тем самым вызывая изменение магнитного поля.[31]
В действительности, верную интерпретацию магнетизма может дать только квантовомеханическоерассмотрение, так как существование элементарных магнитных диполей связано с квантованным орбитальным моментом и спином электронов, а не с классическими токами, которые быстро исчезли бы, например, в магнитных диэлектриках. Электрон со спином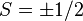 
, может быть охарактеризован магнитным моментом с амплитудой
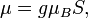
где g — множитель Ланде,[Комм 4] а 
— магнетон Бора. На практике можно измерить лишь одну из трёх компонент вектора магнитного момента (например, проекцию на ось z). Если S — суммарный спин орбитали изолированного атома, то проекция магнитного момента принимает значения[32]
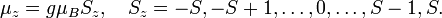
Атом с полным механическим моментом J обладает магнитным моментом с амплитудой
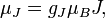
где множитель Ланде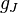 
может быть сложной функцией от орбитальных квантовых чисел электронов атома.[33] Упорядочивание спиновых и орбитальных моментов атомов позволяет наблюдать пара- и ферромагнетизм. Вклад в магнитные свойства веществ дают электроны частично заполненных атомных оболочек. Кроме того, в металлах может быть важным учёт электронов проводимости s-оболочек, магнитный момент которых является делокализированным.[34]
Применимость макроскопического описания [править | править вики-текст]
Являясь квантовыми характеристиками, компоненты оператора спина не коммутируют друг с другом. Однако если ввести оператор среднего спина
где N — количество спинов в системе, то его компоненты будут коммутировать при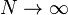 
:
где индексы α, β и γ пробегают по компонентам оператора среднего спина, i — мнимая единица, а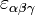 
— символ Леви-Чивиты. Это означает, что систему с достаточно большим количеством спинов можно рассматривать как классическую. Феноменологическое описание возможно применять к системам, где возбуждения имеют многочастичный характер (то есть, обменное взаимодействие должно существенно превышать релятивистскиевзаимодействия, такие как, например, диполь-дипольное).[35]
Напряжённость магнитного поля. Магнитные параметры вещества [править | править вики-текст]
В теореме циркуляции магнитного поля необходимо учесть кроме токов проводимости j молекулярные токи j m (индукция электрического поля для простоты считается нулевой):
| СГС | СИ |
| 
|
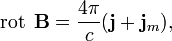
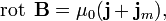
где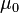 
— магнитная постоянная.
Величину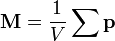 
, характеризующую магнитный момент единицы объема вещества, называют намагниченностью (иногда её обозначают буквой J). Плотность молекулярных токов можно связать с намагниченностью просуммировав их по некоторой площади. Молекулярный ток равен циркуляции магнитного момента по контуру, охватывающему эту площадь. Тогда по теореме Стокса
| СГС | СИ |
 .
|  .
|
Ротор намагниченности равен нулю, когда молекулярные токи в отдельных атомах или молекулах вещества ориентированны таким образом, что компенсируют друг друга.
Обычно вводят вспомогательное векторное поле
| СГС | СИ |
 ,
|  ,
|
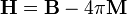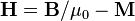называемое напряжённостью магнитного поля. Тогда формула для циркуляции магнитного поля записывается как
| СГС | СИ |
 .
|  .
|
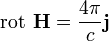В слабых полях намагниченность вещества пропорциональна напряжённости поля, что записывают как
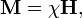
где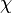 
называют магнитной восприимчивостью. Это безразмерная величина, которая может изменяться в значительном диапазоне значений (к примеру, −2,6·10-5 в серебре[36] и около 2·105в железе чистотой 99,95 %[37]) будучи как положительной, так и отрицательной. Связь между индукцией и напряжённостью магнитного поля можно записать как
| СГС | СИ |
 ,
|  ,
|
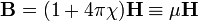где величину 
называют магнитной проницаемостью. В общем случае она является тензорной величиной.[38]
Классы магнитной симметрии [править | править вики-текст]
См. также: Список кристаллографических групп
Отличие между электрическими и магнитными свойствами кристаллов связано с различным поведением токов и зарядов по отношению к изменению знака времени. Обозначим через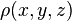 
микроскопическую плотность зарядов в кристалле, а через 
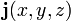— микроскопическую плотность токов в нём, усреднённые по времени. Преобразование временной координаты 
не меняет знака функции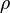 
в отличие от функции 
. Но если состояние кристалла при этом не меняется, то должно выполняться условие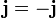 
, откуда следует, что 
. Кристаллы, для которых выполняется это условие не обладают магнитной структурой. Электрическая структура при этом существует всегда, так как нет причин, по которым плотность зарядов обращается в нуль при изменении знака времени.[39] Магнитная структура является малым искажением по отношению к структуре немагнитной фазы и обычно возникает при понижении температуры, поскольку она связана со сравнительно слабыми взаимодействиями глубоко расположенных d- и f-электронов.[40]
Удобней рассматривать симметрию не функции 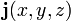, а распределения намагниченности 
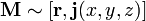.[Комм 5] Она соответствует симметрии расположения усреднённых по времени магнитных моментов в кристаллической решётке. Обозначим операцию преобразования направлений всех токов на противоположное символом R. Классы магнитной симметрии делятся на три типа. К первым двум относятся 32 обычных кристаллических класса и они же, дополненные операцией R. Третий тип составляют 58 классов, в которые R входит только с операциями поворота или отражения. Существует три типа пространственных магнитных групп, объединяющих 1651 группу. Первые два из них, как и в случае магнитных классов, содержат по 230 групп, совпадающих с кристаллографическими без операции R и дополненных ею. Третий класс содержит 1191 группу, в которой R комбинируется споворотами, отражениями или трансляциями.[41]
| Магнитные классы | |
| Ci (C1) | C3v (C3) |
| CS (C1) | D3 (C3) |
| C2 (C1) | D3d (D3, S6, C3v) |
| C2h (Ci, C2, CS) | C3h (C3) |
| C2v (D2, C2h, C2v) | C6 (C3) |
| D2 (C2) | D3h (C3h, C3v, D3) |
| D2h (D2, C2h, C2v) | C6h (C6, S6, C3h) |
| C4 (C2) | C6v (C6, C3v) |
| S4 (C2) | D6 (C6, D3) |
| D2d (S4, D2, C2v) | D6h (D6, C6h, C3v, D3d, D3h) |
| D4 (C4, D2) | Th (T) |
| C4v (C4, C2v) | Oh (T) |
| C4h (C4, C2h, S4) | Td (T) |
| D4h (D4, C4h, D2h, C4v, D2h) | Oh (O, Th, Td) |
| S6 (C3) |
Магнитные кристаллического классы полностью определяют макроскопические магнитные свойства тела. Так спонтанная намагниченность кристалла будет присутствовать, если вектор намагниченности, являясь аксиальным вектором, не будет изменяться при преобразовании данного магнитного кристаллического класса.[42]
Классификация по характеру взаимодействия с магнитным полем [править | править вики-текст]
Магнитными свойствами, выраженными в той или иной степени, обладают все вещества.[43] Причиной взаимодействия с внешним магнитным полем являются собственные или наведённые магнитные моменты, которые ориентируясь определённым образом изменяют поле внутри вещества. Наиболее слабо магнитные эффекты проявляются в диа- и парамагнетиках. Атомы диамагнетиков не обладают собственным магнитным моментом и в соответствии с законом Ленца во внешнем поле внутри них появляются слабые круговые токи, стремящиеся компенсировать его. Атомы парамагнетиков обладают собственными слабыми магнитными моментами, которые при включении внешнего поля ориентируются вдоль него.
Существует несколько классов веществ, в которых взаимодействие между собственными магнитными моментами атомов особо сильное и имеяквантовомеханическую природу принципиально не может быть объяснено с помощью аналогий классической физики. Магнитную структуру в них создает обменное взаимодействие.[44] Вещества, в которых ближайшие магнитные моменты выстраиваются параллельно, называются ферромагнетиками.Антиферромагнетики и ферримагнетики обладают двумя ферромагнитными решётками с противоположными направлениями магнитных моментов, вложенными одна в другую. Различие между ними состоит в том, что решётки в антиферромагнетиках компенсируют друг друга, а в ферримагнетиках магнитные моменты различных решёток различны и суммарный магнитный момент не равен нулю. Говорят, что такие материалы (магнетики) имеютдальний магнитный порядок. Математическое описание магнитных подрешёток[Комм 6] этих трёх классов веществ во многом подобно.
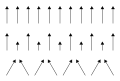
Ферромагнитное упорядочивание
Антиферромагнитное упорядочивание
Ферримагнитное упорядочивание
Также выделяют некоторые искусственные материалы, обладающие ближним магнитным порядком. Спиновые стёкла создаются добавлением магнитных примесей в немагнитные металлы и сплавы. Ансамбли ферро- или ферримагнитных частиц демонстрируют слабые парамагнитные свойства. В таком случае говорят о суперпарамагнетизме.
Магнитные взаимодействия ферро- и антиферромагнетиков [править | править вики-текст]
Модель Гейзенберга [править | править вики-текст]
При описании ферро- и антиферромагнетиков часто применяют модель Гейзенберга. Она заключается в определении магнитной части гамильтонианакристалла в виде
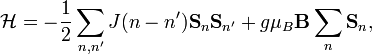
| (ГейзГам) |
где индексы n и n' пробегают по узлам кристаллической решётки, а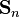 
— оператор спина в n -м узле. Коэффициент 
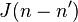называется обменным интегралом, который обеспечивает магнитное упорядочивание изотропного кристалла. На практике полагают, что он существенно отличен от нуля лишь для ближайших соседей. Множитель ½ учитывает повтор при суммировании спинов по решётке (однако иногда его заносят в значение обменного интеграла). При данном выборе знака перед суммой ферромагнитному упорядочиванию соответствует положительное значение 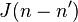, а антиферромагнитному — отрицательное. Второе слагаемое является энергией взаимодействия системы спинов с магнитным полем (Зеемановскаяэнергия), магнитная индукция которого равна B (здесь g — множитель Ланде, — магнетон Бора).[45][46]
Гейзенберовский гамильтониан строится в предположении, что магнитные моменты (и спины, соответственно) локализированы в узлах кристаллической решётки, а орбитальные моменты отсутствуют. Первому условию отвечают ферромагнитные диэлектрики и полупроводники, но для металлов чаще бывает более предпочтительной зонная модель. Допустимость второго условия определяется степенью «замороженности» орибитальных моментов.[47]
Построить микроскопическую модель антиферромагнетиков, аналогичную модели Гейзенберга невозможно, поэтому на макроскопическом уровне их представляют как совокупность нескольких магнитных подрешёток с противоположными направлениями намагниченности, вложенных одна в другую. Это описание хорошо соответствует экспериментальным данным.[48]
Модель Изинга [править | править вики-текст]
Основная статья: Модель Изинга
Обменное взаимодействие [править | править вики-текст]
Основная статья: Обменное взаимодействие
Обменное взаимодействия проявляется вследствие кулоновского отталкивания электронов и принципа Паули. Оно является основной причиной, по которой проявляются ферромагнитные свойства веществ.[49] Так как описывать обменное взаимодействие многоэлектронных систем с помощью микроскопического гамильтониана, учитывающего кинетическую энергию отдельных электронов, непрактично, обычно используют макроскопический гамильтониан, в котором операторы спинов заменяются квазиклассическими векторами спинов в форме Гейзенбергой модели (формула ГейзГам), что является верным для спинов ½. Эмпирически обменный интеграл можно оценить как
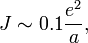
где e — заряд электрона, a — постоянная магнитной решётки.[50] Дать его точную теоретическую оценку очень сложно, поэтому на практике обычно используются экспериментально измеренные значения.[51]
Обобщение, учитывающее обменную анизотропию (X—Y—Z модель) записывается в виде
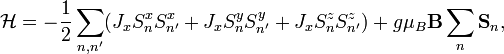
где коэффициенты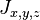 
предполагаются слабо различающимися, так как само по себе обменное взаимодействие изотропно.[52] Макроскопическая плотность энергии для ферромагнетиков, получаемая из Гейзенберовского гамильтониана записывается как
| (МакрОбм) |
где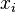 
— координаты физического пространства, M — вектор намагниченности, константа обменного взаимодействия (в общем случае тензор)
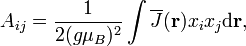
а константа изотропного обмена
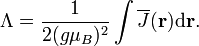
Здесь функцию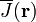 
полагают близкой к обменному интегралу при температурах, далёких от температуры Кюри.[53] Константу A иногда называют константой анизотропного обмена для отличия от 
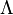. Первое слагаемое в формуле МакрОбм является существенным при рассмотрении неоднородного распределения намагниченности, а второе — для изучения действия механизмов, изменяющих длину вектора намагниченности.[54] Во многих случаях работает механизм не прямого обмена, связывающего спины соседних атомов через перекрытия их волновых функций и Кулоновскую энергию, а косвенного (РККИ-обменное взаимодействие, суперобмен и др.).[55]
Релятивистские взаимодействия [править | править вики-текст]
Взаимодействия элементарных диполей между собою и с электрическим полем самой кристаллической решётки по своей природе являютсярелятивистскими. Отношение их энергий к энергии обменного взаимодействия по порядку величины равно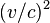 
, где v — скорость электрона в атоме, c — скорость света. Они приводят к установлению статистического равновесия и образованию избранных направлений намагниченности в кристаллах.[56]
Диполь-дипольное взаимодействие и магнитостатическая энергия [править | править вики-текст]
Под диполь-дипольным взаимодействием (англ.)русск. понимают взаимодействие элементарных магнитных диполей между собой. Оно уменьшается пропорционально кубу расстояния и доминирует над обменным взаимодействием на больших расстояниях, являясь причиной макроскопической намагниченности ферромагнетиков.[57] К гамильтониану диполь-дипольного взаимодействия можно прийти, заменив классические диполи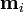 
в формуле энергии взаимодействия двух магнитных моментов
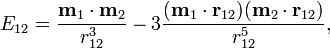
на операторы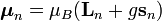 
, где 
— радиус-вектор, соединяющий точки расположения диполей, — магнетон Бора, 
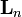— оператор полного орбитального момента, а 
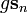— произведение Дираковского фактора Ланде 
и оператора полного спина атома в узле кристаллической решётки под номером n. Тогда гамильтониан дипольного взаимодействия примет вид
где суммирование производится по всем узлам магнитной подрешётки.[58]
Переход к макроскопическому описанию даёт выражение для энергии в форме
Первое анизотропное слагаемое в подынтегральном выражении отражает вариации магнитного поля на расстояниях порядка атомных и зависит черезтензор 
от структуры примитивной ячейки кристалла. Второе и третье слагаемые появляются как решение уравнений магнитостатики.[59]
Магнитная анизотропия [править | править вики-текст]
Основная статья: Магнитная анизотропия
Взаимодействие спинов с электромагнитным полем кристаллической решётки или спин-орбитальное взаимодействие, а также спин-спиновое взаимодействие приводят к появлению магнитной анизотропии. На макроскопическом уровне она наблюдается как энергетическая неэквивалентность различных направлений в кристалле, когда то или иное направление намагниченности по отношению к кристаллографическим осям оказывается более выгодным. В простейшем случае для одноосных ферромагнитных кристаллов, плотность энергии магнитной анизотропии может быть записана в двух эквивалентных формах через нормированный на единицу вектор намагниченности с проекциям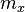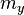и 
, 
и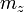 
(эквивалентность здесь означает точность до константы, не зависящей от направления намагниченности):
или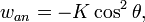 
где коэффициент K называют константой анизотропии, а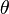 
— угол между направлением вектора намагниченности и главной осью симметрии кристалла. В зависимости от знака K при данном выборе вида энергии говорят о легкоосных (
, намагниченность ориентируется вдоль оси для минимизации энергии: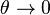 
) и легкоплоскостных магнетиках (
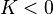, намагниченность ориентируется перпендикулярно оси для минимизации энергии: 
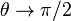).[60]
Кубические кристаллы существенно отличаются от одно- и двухосных по той причине, что их энергия анизотропии определяется членами четвёртого порядка в разложении по компонентам вектора намагниченности, нормированного на единицу:
Вследствие этого, их анизотропия выражена слабее. Для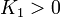 
(например, у железа) минимум энергии достигается в направлениях рёбер куба [100], [010] и [001], то есть существует три эквивалентные оси легкого намагничивания. Иначе осями лёгкого намагничивания будут пространственные диагонали куба.[61]
| Зависимость энергии анизотропии от направления (более насыщенный цвет — больше энергия) | |||||||||||||||
|
Магнитные домены [править | править вики-текст]
Магнитные домены в NdFeB (фотография получена методомКерровской микроскопии)
Основная статья: Домен (магнетизм)
Понятие магнитного домена было введено Пьером Вейсом в 1907 году чтобы дать ответ на вопрос, почему железо будучи ферромагнетиком имеет нулевой магнитный момент при отсутствии внешнего поля. Под ферромагнитными доменами понимают макроскопические области магнитных кристаллов, в которых ориентация вектора спонтаннойнамагниченности различна. Они существуют при температуре ниже точки Кюри.[62] Также говорят об антиферромагнитных доменах, подразумевая вектор антиферромагнетизма вместо намагниченности. Однако их существование, строго говоря, не приводит к выигрышу в энергии и обычно связывается с существованием нескольких зародышей антиферромагнитной структуры со случайным направлением намагниченности при переходе антиферромагнетика через точку Нееля.[63]
Причина появления магнитных доменов в ферромагнетиках была предложена Львом Ландау и Евгением Лифшицем в 1937 году. Они предположили, что их образование приводит к минимизации полной энергии магнетика и поля рассеивания (то есть магнитного поля, создаваемого спонтанной намагниченностью и выходящего за пределы магнетика). Действительно, наблюдаемое на практике направление намагниченности в доменах в обычных условиях формирует замкнутый магнитный поток.[64]
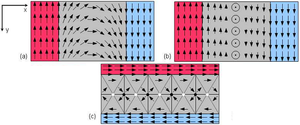
(а) Стенка Нееля. (б) Стенка Блоха (точка в круге означает направление на зрителя). (c) Cross-tie стенка.
Граница между доменами имеет название доменной стенки. Её ширина определяется соотношением между обменной константой и константой анизотропии. В зависимости от результирующего угла поворота намагниченности различают 180°-е, 90°-е и другие доменные стенки. В зависимости от способа поворота намагниченности внутри 180°-х доменных стенок говорят о стенке Блоха и стенкеНееля. Последняя характерна для тонких магнитных плёнок, так как она обладает меньшим полем рассеяния, чем Блоховская стенка.[65]
Существует много методов наблюдения доменов в ферромагнетиках. В 1932 году Фрэнсис Биттерпредложил простой метод визуализации полей рассеивания с помощью коллоидных суспензиймагнитных частиц, не требующий специального оборудования. Он заключается в том, что на поверхность магнетика наносятся магнитные микрочастицы, которые практически не испытывая трения концентрируются в местах наибольшего градиента поля, то есть на границах доменов. Их распределение можно наблюдать в оптический микроскоп.[66]Применяются магнитооптические методы, основанные на поворое поляризации света. Для прозрачных плёнок это эффект Фарадея (изменение поляризации при прохождении сквозь образец), для иных — магнитооптический эффект Керра (изменение поляризации при отражении от образца). Преимуществом Керровской микроскопии является возможность прямого наблюдения доменов, это неразрушающий метод, однако при этом образцы должны быть плоскими, а для повышения контраста необходимо применять дополнительную обработку изображений.[67] Кроме вышеописанных методик, используется ближнепольная микроскопия, рассеяние гамма-лучей и нейтронов, просвечивающая электронная микроскопия и др.[68]
Гистерезис и термодинамика [править | править вики-текст]
Магнитный гистерезис, измеренный в различных полях.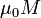 
ост — остаточная намагниченность, H коэр — коэрцитивная сила
Движение магнитного момента [править | править вики-текст]
Уравнение Ландау — Лифшица [править | править вики-текст]
Основная статья: Уравнение Ландау — Лифшица (магнетизм)
Магнетизм диэлектриков и полупроводников [править | править вики-текст]
Диэлектрик Мотта — Хаббарда [править | править вики-текст]
В диэлектриках и полупроводниках нет коллективизированных электронов в отличие от металлов. Следствием является локализация магнитных моментов вместе с электронами на ионных состояниях. Это является основным отличием магнетизма диэлектриков от магнетизма металлов, который описывается зонной теорией.[69]
Согласно зонной теории, диэлектриками могут кристаллы, содержащие в примитивной ячейке чётное количество электронов. Это означает, что диэлектрики могут быть лишь диамагнетиками, что не объясняет свойств многих веществ. Причинойпарамагнетизма Кюри (парамагнетизм локализованных электронов), ферро- и антиферромагнетизма диэлектриков является кулоновское отталкиваниеэлектронов, что объясняется моделью Хаббарда на следующем примере. Появление дополнительного электрона в изолированном атоме увеличивает его энергию на некоторую величину 
. Следующий электрон попадёт на энергетический уровень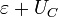 
, где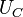 
— энергия кулоновского взаимодействия электронов, в реальных атомах колеблющаяся от 1 эВ до более чем 10 эВ. В кристалле энергетические уровни этих двух электронов расщепятся на зоны и кристалл будет диэлектриком или полупроводником, пока между ними существует запрещённая зона. Вместе обе зоны могут содержать чётное число электронов, но может быть ситуация, когда заполнена только нижняя зона и в ней находится нечётное число электронов. Диэлектрик, для которого выполняется это условие, называется диэлектриком Мотта — Хаббарда. Если интегралы перекрытия малы, диэлектрик будет парамагнетиком, иначе — антиферромагнетиком.[70] За ферромагнетизм таких диэлектриков, как EuO или CrBr3, отвечает суперобменное взаимодействие.[71]
Суперобменное и антисимметричное обменное взаимодействия [править | править вики-текст]
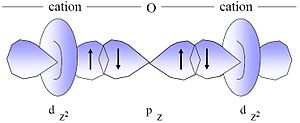
Схема суперобменного взаимодействия в антиферромагнетике
Большинство ферро- и ферримагнитных диэлектриков состоит из магнитных 3d-ионов, разделённых такими немагнитными ионами, как O2−, Br−, Cl− и др. Образуется ситуация, когда расстояния для непосредственного взаимодействия 3d-орбиталей слишком велико и обменное взаимодействие осуществляется перекрытием волновых функций 3d-орбиталей магнитных ионов и p-орбиталей немагнитных ионов. Орбитали оказываются гибридизированными, а их электроны становятся общими для нескольких ионов. Такое взаимодействие называется суперобменным. Его знак (то есть, является ли диэлектрик ферро- или антиферромагнетиком) определяется типом d-орбиталей, количеством электронов на них и углом, под которым видна пара магнитных ионов из узла, где находится немагнитный ион.[72]
Антисимметричное обменное взаимодействие (взаимодействие Дзялошинского — Мория) между двумя ячейками с векторами спина 
и 
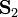описывается выражением
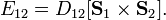
Очевидно, энергия взаимодействия ненулевая только если ячейки не магнитно эквивалентны. Взаимодействие Дзялошинского — Мория проявляется в некоторых антиферромагнетиках. Результатом является появление слабой спонтанной намагниченности. Этот эффект называют слабым ферромагнетизмом, так как результирующая намагниченность составляет десятые доли процентов от намагниченности в типичных ферромагнетиках. Слабый ферромагнетизм проявляется в гематите, карбонатах кобальта, марганца и некоторых других металлов.[73][5][74]
Магнетизм металлов [править | править вики-текст]
Зонный магнетизм [править | править вики-текст]
| Различие между зонной структурой магнитных и немагнитных металлов на примере меди и кобальта. Электронная зонная структура (слева) и плотность состояний (справа) на каждой из схем. | |||||||||||||||
|
Обменные взаимодействия в металлах [править | править вики-текст]
Обменное взаимодействие в металлах может осуществляться принципиально различными механизмами, зависящим от типа атомных орбиталей, отвечающих за обменное взаимодействие. У таких переходных 3d-металлов как железо или кобальт, определяющую роль в обмене играет перекрытие 3d-волновых функций соседних атомов в кристаллической решетке, в то время, как у 4f-элементов обменное взаимодействие происходит посредствомэлектронов проводимости. Манганиты лантана обладают сложной зависимостью магнитных свойств от степени их легирования.[75]
3d-металлы [править | править вики-текст]
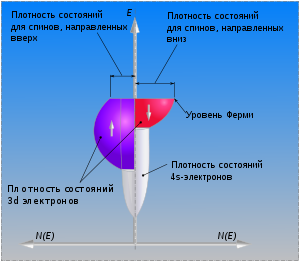
Плотность электронных состояний на уровне Ферми для 3d-электронов с различным направлением спина различна, а для 4s-электронов — одинакова.
См. также: Гигантское магнетосопротивление#Спин-зависимое рассеяние
3d-металлы характеризуются значительной энергией кулоновского взаимодействия между электронами 3d-зоны по сравнению с их кинетической энергией.[76] Оно же фактически является причиной ферромагнитного упорядочивания.[77] Как для 3d-, так и для 4f-элементов их магнитное упорядочивание зависит от степени заполнения соответствующей зоны. Переходной 3d-металл будет ферромагнетиком, если его 3d-зона содержит малое количество электронов или дырок (то есть она должна быть или слабо заполнена, или заполнена почти полностью). Это хорошо иллюстрируется железом, кобальтом иникелем, где эта зона почти полностью заполнена. Антиферромагнитное состояние будет основным, если она заполнена наполовину.[76]
Условие, определяющее, будет ли металл ферро- или антиферромагнетиком, связано с тем, что электрону выгодно быть делокализованным, так как согласно принципу неопределённостей Гейзенберга, это позволяет уменьшить его кинетическую энергию. Качественно, его можно объяснить следующим образом. Для электронов должно соблюдаться правило Хунда (суммарный спин электронов на орбитали должен быть максимальным). Тогда для зоны, к примеру, заполненной меньше, чем наполовину, электроны двух соседних атомов могут иметь одинаковое направление спина, но разные магнитные квантовые числа, что и определяет ферромагнитное упорядочивание. В случае наполовину заполненной зоны, 3d-электроны соседних атомов вынуждены иметь противоположное направление суммарного спина для того, чтобы поделить между собой одинаковые магнитные числа.[78]
4f-металлы [править | править вики-текст]
Основная статья: РККИ-обменное взаимодействие
Редкоземельные элементы имеют частично заполненную 4f-орбиталь, характерный размер которой существенно меньше межатомных расстояний в кристаллической решётке. Поэтому 4f-электроны соседних ионов не могут напрямую взаимодействовать друг с другом. Обменное взаимодействие между ними осуществляется с помощью электронов проводимости. Каждый редкоземельный ион создает возле себя достаточно сильное эффективное поле, которое поляризует электроны проводимости. Такое непрямое обменное взаимодействие между 4f-электронами называют взаимодействием Рудермана — Киттеля — Касуя — Иосиды (РККИ-обменное взаимодействие).[79] Будет ли металл ферро- или антиферромагнетиком зависит от строения 4f-зоны и расстояния между ионами Зависимость обменного интеграла от произведения волнового вектора электронов на уровне Ферми k F и расстояния между магнитными ионами a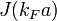 
имеет знакомпеременный осциллирующий характер. Этим, в частности, объясняется существованиегеликоидальных и некоторых других магнитных структур. РККИ-взаимодействие существенно зависит от концентрации свободных носителей заряда и может быть существенно более дальнодействующим, чем прямой обмен.[80]
Двойной обмен [править | править вики-текст]
Оксиды переходных металлов могут быть как проводниками, так и диэлектриками. В диэлектриках имеет место суперобменное взаимодействие. Однако управляя легированием можно добиться перехода оксида в проводящее состояние. В манганитах лантана вида La1−xCaxMnO3 при определённых значениях параметра x про часть ионов марганца может иметь валентность 3+, а другая — 4+. Обменное взаимодействие между ними, совершаемое через ионы O2-, называют двойным обменом. Эти соединения так же будут ферро- или антиферромагнетиками в зависимости от значения x. Ферромагнитное упорядочивание будет в том случае, если суммарные спины 3-х и 4-валентных ионов сонаправлены, при этом 4-й электрон может быть делокализован. Иначе он локализирован на ионе с меньшей валентностью. Для La1−xSrxMnO3 переход из антиферромагнитной в ферромагнитную фазы происходит при 
(бо́льшим значениям x соответствует ферромагнетик).[81]
Сверхпроводимость [править | править вики-текст]
Основная статья: Сверхпроводимость
Магнитные жидкости [править | править вики-текст]
Основная статья: Ферромагнитная жидкость
Магнитная жидкость на поверхности стекла под воздействием сильного магнитного поля
Биомагнетизм[править | править вики-текст]
Чувствительность живых организмов к магнитному полю [править | править вики-текст]
Магнитное поле Земли служит для ориентации в пространстве многим видам животных. По до конца не выясненным причинам, птицы и черепахи используют информацию о магнитном наклонении, а лососевые, и рукокрылые реагируют на горизонтальную компоненту поля.[82] «Компас» птиц в нормальном режиме функционирует в интервале полей от 43 до 56 мкТ, но после адаптации способен воспринимать поля от 16 до 150 мкТ.[83] При этом птицы не различают северный и магнитный полюса и нуждаются в дополнительной световой информации для ориентирования.[84] Чувствительными к магнитному полю также являются морские моллюски, саламандры (например, Eurycea lucifuga(англ. Spotted-tail Salamander)), тритоны (например, зеленоватый тритон), шершни, медоносные пчёлы и аллигаторы.[85][86]
Существуют различные рецепторы, реагирующие на внешнее магнитное поле. В глазах дрозофил и некоторых птиц содержатся молекулы криптохрома, некоторые другие (например, бурая летучая мышь (англ. Big brown bat)) содержат в своём теле однодоменные частицы. Некоторые бактерии используют специальные органеллы — магнетосомы. В то же время, многие животные способны определять поляризацию солнечного света и ориентироваться по звёздам. Поэтому, несмотря на доказанное умение многих видов применять магнитные поля для определения направления, однозначного ответа на вопрос, как именно ориентируется в пространстве то или иное животное находясь в дикой природе, на данное время нет.[87]
Эффективность воздействия электромагнитных полей на живые организмы связана с наличием «окон чувствительности» по амплитуде, градиенту и частоте, иногда специфическое воздействие может оказать последовательность сигналов определённой формы.[88] Внутренний компас животных может быть связан с наличием в организме частиц магнетита, например, в форме ферритина. Магнетит также встречается в мозге человека, и в ещё большей концентрации в мозге птиц. Человеческий мозг содержит около 5 миллионов кристаллов на грамм, а в его мембранах содержится около 100 миллионов кристаллов на грамм. Отклик магнетита на магнитное поле более чем в миллион раз превышает отклик обычной пара- или диамагнитной среды и, предположительно, это может оказывать влияние на транспорт ионов между клетками.[83] Чувствительность шишковидного тела в мозге млекопитающих к магнитным полям связана с функционированием сетчатки глаза. Это приводит к тому, что сетчатка включается в магниторецептивную систему организма. Её роль иллюстрируется тем фактом, что при ослаблении градиента магнитного поля Земли до 30 нТ/м, у большинства людей снижаетсяпорог восприятия мерцающего света, как постоянного (англ. Flicker fusion threshold).
Магнетотаксис [править | править вики-текст]
Основная статья: Магнетотаксис
Существует несколько видов анаэробных бактерий (магнетотактические бактерии (англ. Magnetotactic bacteria): Aquaspirillum mangetotacticum и др.), способных реагировать на внешние магнитные поля. Они содержат органелы, называемые магнетосомами, в мембранах которых содержатся однодоменные кристаллы магнетита Fe3O4 или мельниковита Fe3S4 (иногда и те, и другие вместе). Размер кристаллов колеблется колеблется от 40 до 100 нм. Магнетосомы образуют цепочки, закреплённые внутри бактерии таким образом, что направление намагниченности магнитных нанокристаллов совпадает с направлением цепочек.[89]
Магнетотактические бактерии являются природными компасами, которые ориентируются вдоль направления магнитного поля Земли. Благодаря тому, что они реагируют на слабые поля напряженностью порядка 0,5 эрстед, они используются в скоростных высокочувствительных методах визуализациидоменной структуры магнетиков (например, для проверки трансформаторной стали). При помещении магнетотактических бактерий на магнитную поверхность они за несколько секунд перемещаются вдоль силовых линий к северным полюсам скапливаясь в местах, где магнитное поле перпендикулярно поверхности. Методы с применением магнетотактических бактерий дают лучший контраст чем классический метод Биттера иликонтраст стенок. Естественным ограничением их разрешения служит размер бактерии порядка одного микрометра.[90]
Геомагнетизм[править | править вики-текст]
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур[2][3][4].
В формуле
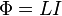
— магнитный поток, 
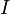— ток в контуре, 
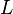— индуктивность.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:
.
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции (в вольтах), возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:
.
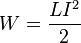Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности[4]. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников[5].
Для имитации индуктивности, то есть ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются[6] и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определённую эффективную индуктивность, используемую в расчётах полностью (хотя вообще говоря с определёнными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.
Содержание
[убрать]
Обозначение и единицы измерения[править | править вики-текст]
В системе единиц СИ индуктивность измеряется в генри[7], сокращённо «Гн». Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт.
В вариантах системы СГС — системе СГСМ и в гауссовой системе индуктивность измеряется в сантиметрах (1 Гн = 109 см; 1 см = 1 нГн)[4]; для сантиметров в качестве единиц индуктивности применяется также название абгенри. В системе СГСЭ единицу измерения индуктивности либо оставляют безымянной, либо иногда называют статгенри (1 статгенри ≈ 8,987552×1011 генри: коэффициент перевода численно равен 10−9 от квадрата скорости света, выраженной в см/с).
Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца(Heinrich Friedrich Emil Lenz)[8][9]. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry)[10]. Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года[11].
Теоретическое обоснование[править | править вики-текст]
Если в проводящем контуре течёт ток, то ток создаёт магнитное поле[4].
Будем здесь вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля не настолько сильны и быстры, чтобы ими нельзя было пренебречь в смысле порождения ими магнитного поля.
Ток считаем одинаковым по всей длине контура (пренебрегая ёмкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину).
По закону Био — Савара — Лапласа, величина вектора магнитной индукции, создаваемой некоторым элементарным (в смысле геометрической малости участка проводника, рассматриваемого как элементарный источник магнитного поля) током в каждой точке пространства, пропорциональна этому току. Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле (вектор магнитной индукции), создаваемое всем проводником, также пропорционально порождающему току.
Рассуждение выше верно для вакуума. В случае присутствия магнитной среды[12] (магнетика) с заметной (или даже большой) магнитной восприимчивостью, вектор магнитной индукции (который и входит в выражение для магнитного потока) будет заметно (или даже во много раз) отличаться от того, каким бы он был в отсутствие магнетика (в вакууме). Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший (или уменьшившийся) в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остаётся пропорциональным порождающему его току.
Тогда магнитный поток, то есть поток поля вектора магнитной индукции:
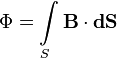
через любую конкретную фиксированную поверхность S (в частности и через интересующую нас поверхность, краем которой является наш контур с током) будет пропорционален току, так как пропорционально току B всюду под интегралом.
Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной. На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближённо рассчитать поток через неё (а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже). Однако здесь, при чисто теоретическом рассмотрении нет необходимости во введении каких-то дополнительных упрощающих представлений, достаточно просто заметить, что как бы ни был сложен контур, в данном параграфе мы имеем в виду «полный поток» — то есть поток через всю сложную (как бы многолистковую) поверхность, натянутую на все витки катушки (если речь идет о катушке), то есть о том, что называется потокосцеплением. Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует (ведь свойство пропорциональности току сохраняется для любой).
Итак, мы обосновали:
~ 
этого достаточно, чтобы утверждать, введя обозначение L для коэффициента пропорциональности, что
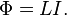
В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур. (Действительно, даже на самый простой контур может быть натянута — в том смысле, что контур должен быть её краем — не единственная поверхность, а разные, например, начав с двух совпадающих поверхностей, затем одну поверхность можно немного прогнуть, и она перестанет совпадать со второй). Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур.
Но это действительно так: возьмём две такие поверхности. Вместе они будут составлять одну замкнутую поверхность. А мы знаем (из закона Гаусса для магнитного поля), что магнитный поток через любую замкнутую поверхность равен нулю. Это (с учетом знаков) означает, что поток через одну поверхность и другую поверхность — равны. Что доказывает корректность определения.
Свойства индуктивности[править | править вики-текст]
Индуктивность одновиткового контура и индуктивность катушки[править | править вики-текст]
Величина магнитного потока, пронизывающего одновитковый контур, связана с величиной тока следующим образом[4]:
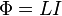
где 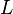— индуктивность витка. В случае катушки, состоящей из N витков предыдущее выражение модифицируется к виду:
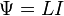
где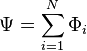 
— сумма магнитных потоков через все витки (это так называемый полный поток, называемый в электротехнике потокосцеплением, именно он фигурирует в качестве магнитного потока вообще в случае для катушки в общем определении индуктивности и в теоретическом рассмотрении выше; однако для упрощения и удобства для многовитковых катушек в электротехнике пользуются отдельным понятием и отдельным обозначением), а — уже индуктивность многовитковой катушки. 
называют потокосцеплением или полным магнитным потоком[15]. Коэффициент пропорциональности иначе называется коэффициентом самоиндукции контура или просто индуктивностью[4].
Если поток, пронизывающий каждый из витков одинаков (что довольно часто можно считать верным для катушки в более или менее хорошем приближении), то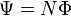 
. Соответственно, 
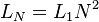(суммарный магнитный поток через каждый виток увеличивается в N раз — поскольку его создают теперь N единичных витков, и потокосцепление ещё в N раз, так как это поток через N единичных витков). Но в реальных катушках магнитные поля в центре и на краях отличаются, поэтому используются более сложные формулы.
Индуктивность соленоида[править | править вики-текст]
Катушка в форме соленоида (конечной длины).
Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока (или магнитная индукция) 
, которая выражается в системе СИ в тесла [Тл], внутри катушки является фактически постоянной и (приближённо) равна
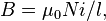
Дата добавления: 2015-08-21; просмотров: 176 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства уравнений Максвелла. | | | Композиция готова! |
)
