Классификация приближений Максвелла уравнений

Классификация приближений M. у. обычно основывается на безразмерных параметрах, определяющих и критерииподобия для эл.-магн. полей. В вакууме таким параметром является отношени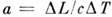е , где - характерный масштаб изменения полей (либо размер области, в к-рой ищется решение), - характерный временной масштаб изменения полей.

а) а = 0 - статич. приближение, статика.

Система M. у. распадается на три.

I.

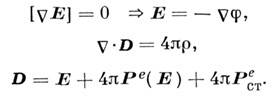
Материальная связь в простейшем случае имеет вид 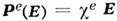. Это система M. у. для электростатики, в к-рой источниками служат заданные распределения плотности электрич. заряда и сторонней поляризации 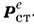. В однородной среде эл.-статич. потенциал f определяется Пуассона уравнением

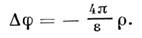
Для более сложных материальных <ур-ний различают электростатику анизотропных сред , нелинейную электростатику 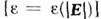, электростатику сред с пространственной дисперсией 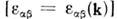, важным частным случаем к-рых являются движущиеся среды с временной дисперсией (здесь может даже меняться тип ур-ния для потенциала с эллиптического на параболический) и т. п.

II. Поля в магнитостатике описываются ур-ниями

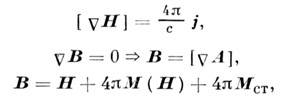
где в случае простейшей материальной связи индуци-ров. намагниченность определяется соотношением

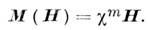
Источниками в ур-ниях магнитостатики являются заданные распределения плотности электрич. тока 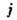и сторонней намагниченности 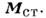В однородной среде

векторный потенциал магн. поля 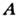(калибровка кулоновская) определяется векторным ур-нием Пуассона

В общем случае возможны такие же разновидности сред, что и в электростатике.

III. K статич. электродинамике относят и процессы протекания пост, токов в распределённых проводящих средах. Токовая статика охватывается ур-ниями

Источниками являются силы неэлектрич. происхождения, действующие на заряды, характеризующиеся напряжённостью 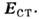Электрич. заряды присутствуют лишь в местах неоднородности среды, напр, на границах проводящих сред. Распределение токов в проводящих средах сопоставимо с распределением электрич. и магн. полей в электростатике и магнитостатике. Часто благодаря этой аналогии говорят, напр., о магн. цепях, по к-рым "текут" магн. потоки 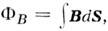аналогичные электрич. токам 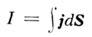в электрич. цепях.

б) - квазистатика, обобщающая соответствующие статич. приближения.

В квазиэлектростатике вакуумные электрич. поля описываются ур-ниями статики (I.), а в ур-ниях для магн. поля в качество заданного источника фигурирует и ток смещения. Квазимагнитостатика описывается статич. ур-ниями для магн. полей с учётом закона индукции (2) для электрич. поля. Поскольку вихревое электрич. поле меняет электрич. токи в проводниках, являющиеся источниками магн. поля, то этот раздел квазистатики более богат, чем предыдущий; он описывает широкий круг явлений, происходящих в цепях перем, тока с сосредоточенными параметрами: ёмкостями, индуктивностями и сопротивлениями.

Квазистатика в распределённых проводящих средах описывается ур-ниями квазистационарного (квазистатического) приближения, в к-рых током смещения пренебрегают по сравнению с токами проводимости. В этом приближении распределения электрич. токов, электрич. и магн. полей описываются одинаковыми ур-ниями диффузионного типа:

Эти ур-ния определяют, напр., распределение токов Фуко, проникновение перем. эл.-магп. поля в проводник (скин-эффект)и т. п.

в) Резонансные волновые поля описываются точной системой M. у., однако их иногда выделяют из общего класса полей, особенно в тех случаях, когда их структура (пространственное распределение) фиксируется границами области, внутри к-рой эти поля могут быть возбуждены (напр., внутри полых резонаторов с металлическими стенками или в поперечном сечении волноводов либо в окрестности тонкой проволочной или щелевой антенны). При этом обычно обращаются к фурье-преобразованию M. у. и представлению поля в виде набора дискретных или квазидискретных мод.

г) . В рамках этого неравенства существуют ква-зиоптич. и оптич. приближения (см. Квазиоптика, Геометрической оптики метод), относящиеся к протяжённым в масштабе длины волны распространениям полей (волновым пучкам, многомодовым конфигурациям и т. п.). Под характерным масштабом, входящим в параметр а, здесь подразумевается масштаб изменения амплитуды поля.

15. Максвелла уравнения в различных системах единиц

Выше использовалась симметричная гауссова абс. система единиц. Удобство гауссовой системы единиц состоит в том, то все 4 вектора поля обладают в ней одинаковыми размерностями и потому в классическом "линейном" вакууме можно избежать введения ненужных констант: в силу безразмерные проницаемости вакуума обращаются в единицы 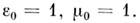Др. достоинством одинаковой размерности эл.-магн. полей является их ес-теств. объединение в единые тензоры поля вида (13), (14) без внесения корректирующих множителей.

Если принять запись ур-ния непрерывности в форме (5), а также соблюдение принципа дуальной симметрии, то M. у. можно придать вид

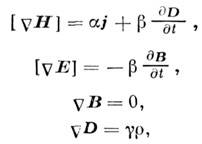
где константы связаны соотношением

Для простейших материальных связей типа (10) можно ввести проницаемости вакуума и относит, проницаемости среды 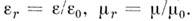Тогда из волнового ур-ния в вакууме следует естеств. соотношение между константами

где с - скорость распространения любого эл.-магн. возмущения (в частности, света) в вакууме. В гауссовой системе

Существует операция рационализации, предложенная Хевисайдом и состоящая в устранении иррациональных числовых множителей из M. у. Простейший путь принят в рационализов. системе Xe-висайда - Лоренца.

В Международной системе единиц (СИ) возникает дополнительная размерная константа, наз. импедансом (или характеристическим сопротивлением) вакуума 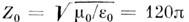Ом. Это представляет известные удобства при сопоставлении процессов распространения плоских волн в свободном пространстве с волнами напряжения и тока в линиях передач, но приходится приписывать вакууму размерные значения проницаемостей:

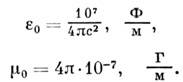
Значения коэф. в СИ: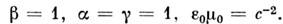

Лит.: Ландау Л. Д., Лифшиц E. M., Теория поля, 7 изд., M., 1988; их же, Электродинамика сплошных сред, 2 изд., M., 1982; Власов А. А., Макроскопическая электродинамика, M., 1955; Никольский В. В., Теория электромагнитного поля, 3изд., M., 1964; Джексон Д ж., Классическая электродинамика, пер. с англ., M., 1965; Каценеленбаум Б. 3., Высокочастотная электродинамика, M., 1966; Стражев В. И., Томильчик Л. M., Электродинамика с магнитным зарядом, Минск, 1975; Медведев Б. В., Начала теоретической физики, M., 1977; Новожилов Ю. В., Яппа Ю. А., Электродинамика, M., 1978; Туров E. А., Материальные уравнения электродинамики, M., 1983; Fущич В. И., Hикитин А. Г., Симметрия уравнений Максвелла, К., 1983; Бредов M. M., Румянцев В. В., Tоптыгин И. H., Классическая электродинамика, M., 1985.

M. А. Миллер, E, В. Суворов.

I. Токи смещения. Опыт Эйхенвальда.

Под током мы понимаем направленное движение электрически заряженных частиц (электронов, ионов) в среде. Но электрический ток можно получить и при движении зарядов вместе с перемещающимися макроскопическими телами. Токи при этом возникающие, называют конвенционными токами.

Электрический ток может быть получен также при движении диэлектрика в поле переменной полярности. Движение зарядов, представляющее собой смещение их в молекулах диэлектрика, называют током смещения.

Опыты по исследованию магнитного поля конвенционных токов и токов смещения провёл в 1901-1903 г.г. русский учёный А.А. Эйхенвальд. Мы остановимся только на токах смещения.

Диэлектрический диск D вращается между четырьмя неподвижными заряженными полудисками. При прохождении плоскости ав происходит смена знаков заряда на сторонах диска, что эквивалентно движению “+” зарядов слева направо, что и показано на чертеже – ток i.

Опытами А.А. Эйхенвальда установлено, что токи смещения, как и токи проводимости, создают такое же магнитное поле. Токи смещения наблюдаются в конденсаторе, включённом в цепь переменного тока. Для постоянного тока конденсатор, включённый в цепь последовательно, является бесконечно большим сопротивлением. Если цепь с конденсатором питать переменным током, то в цепи за каждый период протекают токи заряда и разряда конденсатора, сопротивление которого теперь не бесконечно велико, а зависит от ёмкости конденсатора и частоты тока:

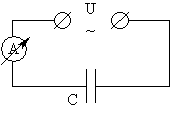
Согласно воззрениям Фарадея-Максвелла, конденсатор надо рассматривать не как разрыв цепи, а как участок цепи с другим механизмом проводимости. Рассмотрим процессы, протекающие в схеме. Генератор переменного тока, напряжение которого U заряжает конденсатор ёмкости С. Заряд конденсатора: Q = CU.

Пусть конденсатор плоский:

Величина зарядного тока, который протекает через конденсатор, в цепи:

, но электрическая индукция:

,

где – вектор поляризации.

(1)

Из (1) следует, что ток смещения состоит из двух слагаемых:

а) – тока смещения, вызванного смещением молекулярных зарядов в диэлектрике (токи поляризации);

б) – тока смещения, определяемого скоростью изменения напряжённости поля, эта составляющая существует в вакууме (т.е. следует, что любое переменное электрическое поле порождает магнитное поле).

В проводящей среде полный ток складывается из суммы тока проводимости и тока смещения:

(2)

Дата добавления: 2015-08-21