Материальные уравнения

В макроэлектродинамике материальные связи, характеризующие эл.-магн. свойства сред, вводятся феноменологически; они находятся либо непосредственно из эксперимента, либо на основании модельных представлений. Существуют два способа описания: в одном векторы E и H считаются исходными и материальные ур-ния задаются в виде D = D (E, H)и В = В (Е, <Н), в другом - за исходные берутся векторы 2-го "блока" E и В, и соответствующие материальные связи представляются иначе: D = D (E,В), H= H (E, В ). Оба описания совпадают для вакуума, где материальные уравнения вырождаются в равенства D = E и B = H.

Рассмотрим простейшую модель среды, характеризуемую мгновенным, локальным поляризац. откликом на появляющиеся в ней поля E и H. Под действием поля E в такой среде возникает электрич. поляризация (см. Поляризации вектор), а под действием поля H - магн. поляризация . Чаще её наз. намагниченностью и обозначают М.

Материальные ур-ния для таких сред имеют вид

При этом индуцированные в среде электрич. заряды наз. связанными или поляризац. зарядами с плотностью , а токи, обусловленные их изменениями,- поляризац. токами с плотностью :

Эти понятия были перенесены и на магн. поля, что можно выразить в виде системы ур-ний, аналогичной

(8):

и только потом выяснилось, что истинными источниками намагничивания среды оказались электрич. токи , а не магн. заряды. Поэтому терминология сложилась на основе физически некорректной системы

тогда как следовало бы принять беззарядовые ур-ния

что равносильно замыканию исходных M. у. (1) - (4) с помощью материальных связей

Из (6) и (7a) следует, что 2-й вариант представления материальных соотношений, в к-ром постулируются в качестве исходных векторы E и B, физически предпочтительнее.

В модели Лоренца - Максвелла усреднение микрополя Н микро, произведённое с учётом вклада со стороны индуциров. полей, приводит к ур-ниям (9) и соответственно < Н микро>= В. Однако обычно параметры сред вводятся с помощью ур-ний (7), что облегчает двойственную симметризацию ф-л (подробнее см. в разделе 9). Напр., скалярные восприимчивости сред (c^e, c^m) определяются соотношениями

и позволяют ввести диэлектрическую проницаемость e и магнитную проницаемость m:

Простейшие модели сред характеризуются пост, значениями В случае вакуума 0.

Классификация разл. сред ооычно основывается на материальных ур-ниях типа (10) и их обобщениях. Если проницаемости e и m не зависят от полей, то M. у. (1) - (4) вместе с материальными ур-ниями (10) остаются линейными, поэтому о таких средах говорят как о линейных средах. При наличии зависимостей среды наз. нелинейными: решения M. у. в нелинейных средах не удовлетворяют принципу суперпозиции. Если проницаемости зависят от координат то говорят о неоднородных средах, при зависимости от времени - о нестац попарных средах (иногда такие эл.-динамич. системы наз. параметрическими). Для анизотропных сред скаляры e, m в (10) заменяются на тензоры: (по дважды встречающимся индексам производится суммирование). Важное значение имеют также эффекты запаздывания и нелокальности отклика среды на внеш. поля.

Значение индуциров. поляризации Р ^е, напр, в момент г, может определяться, вообще говоря, значениями полей во все предыдущие моменты времени, т. е.

что при преобразовании Фурье по времени приводит к зависимости [соответственно i]. Такие среды наз. средами с временной (частотной) дисперсией или просто диспергирующими средами. Аналогичная связь устанавливается и для нелокальных взаимодействий, когда отклик в точке г зависит от значения полей, строго говоря, во всех окружающих точках но обычно всё-таки в пределах нек-рой конечной её окрестности: При преобразовании Фурье по г это приводит к появлению зависимостей такие среды наз. средами с пространственной дисперсией (см. Дисперсия пространственная).

В проводящих средах входящая в M. у. (1) - (5) плотность тока состоит из двух слагаемых: одно по-прежнему является сторонним током обусловленным заданным перемещением электрич. зарядов под действием сторонних сил (обычно неэлектрич. происхождения), а другое - током проводимости зависящим от полей, определяемых системой M. у., и связанным с ними материальными ур-ниями вида В простейшем случае эта зависимость сводится к локальному Ома закону,

где - электропроводность (проводимость) среды. Иногда в (11) вводят обозначение 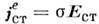, благодаря к-рому различают системы с заданными токами и системы с заданными полями (напряжениями). Для синусоидальных во времени полей, подчинённых ур-ниям (1б) - (4б) и материальным связям (10) и (11), вводится комплексная диэлектрич. проницаемость, объединяющая (10) и (11), , мнимая часть к-рой обусловлена проводимостью и определяет диссипацию энергии эл.-магн. поля в среде. По аналогии вводится комплексная магн. проницаемость , мнимая часть к-рой обусловливает потери, связанные с перемагничиванием среды. Комплексные проницаемости в общем случае зависят от частоты w и волнового вектора эти зависимости не могут быть произвольными: причинности принцип связывает их действительные и мнимые части Крамерса - Кронига соотношениями.

В общем случае вид материальных ур-ний зависит также и от системы отсчёта, в к-рой эти ур-ния рассматривают. Так, если в неподвижной системе К среда характеризуется простейшими ур-ниями (10), то в инер-циальной системе К', движущейся относительно К с пост, скоростью и, появляется анизотропия:

где индексы обозначают продольные и поперечные к составляющие векторов. В рамках алгебраич. M. у. (1в) - (4в) материальные ур-ния (12) могут быть переписаны в виде

что можно трактовать как наличие временной и пространственной дисперсии. Исследование процессов с материальными связями типа (12) составляет предмет электродинамики движущихся сред. Заметим, что хотя характеристики е и m удобно симметризуют материальные ур-ния, их введение не является непременным условием замыкания M. у. Соответствующей перенормировкой допустимо свести описание магн. поля к одно-векторному, т. е. сделать но при этом даже для изотропной среды диэлектрич. проницаемость становится тензором, она различна для вихревых и потенциальных полей. Физически это связано с неоднозначностью модельного представления диполь-ных моментов, во всяком случае при они могут равноправно интерпретироваться и как зарядовые, и как токовые.

---

Дата добавления: 2015-08-21