Анализ уравнения температурного поля для случая охлаждения (нагревания) бесконечной пластины

Из уравнения (12.20) следует, что в условиях охлаждения пластины для любого момента времени при заданных граничных условиях поле температуры имеет вид симметричной кривой с максимумом на оси пластины при Х = 0 (для нагревания – с минимумом на оси). Для каждого последующего момента времени будет своя кривая, монотонно убывающая к поверхностям пластины. При этом для любого момента времени касательные к кривым в точках Х = ± 1 проходят через две направляющие точки + А и – А – расположенные на расстоянии х₀ от поверхности пластины. Причем х₀ = 1/ Bi (рис. 12.4).

Рисунок 12.4 Изменение температурного поля в плоской неограниченной пластине при ее охлаждении

Такое свойство температурных кривых дает возможность определить характер изменения температуры в теле при заданном Bi. Рассмотрим следующие случаи.

1) Случай, когда Bi → ∞ (практически Bi >100). Т.к. , то Bi → ∞, когда α → ∞, т.е. когда имеет место очень большая интенсивность отвода теплоты от поверхности и температура поверхности пластины становится сразу равной температуре окружающей среды, в которую помещена пластина. В этих случаях процесс охлаждения определяется физическими свойствами и размерами тела, т.е. его внутренним термическим сопротивлением - внутренняя задача.

В этом случае при Fo ≥ 0,3 из уравнения (12.20) с учетом только первого члена ряда можно получить уравнение для определения времени прогрева середины пластины до заданной температуры:

. (12.21)

Рисунок 5 Распределение температуры в пластине при ее охлаждении в условиях Bi → ∞ и Fo₁ < Fo₂ < Fo₃….

2) Случай, когда Bi → 0 (практически Bi < 0,1). Это возможно при малых толщинах пластины и очень малом коэффициенте теплоотдачи с поверхности пластины, теоретически когда α → 0.

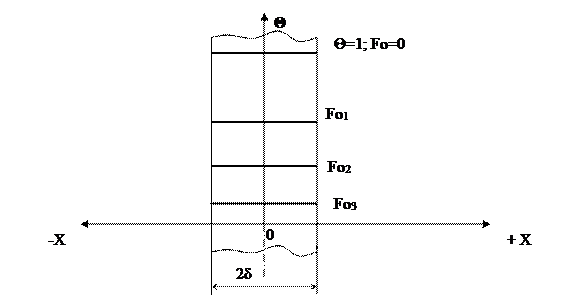
Рисунок 12.6 Распределение температуры в пластине при ее охлаждении в условиях при Bi → 0 и Fo₁ < Fo₂ < Fo₃….

При малых значениях Bi температура на поверхности пластины при ее остывании незначительно отличается от температуры на оси, т.е. температура по толщине пластины распределяется равномерно и кривая температуры параллельна оси абсцисс. В рассматриваемом случае процесс охлаждения (или нагрева) тела определяется интенсивностью теплоотдачи на поверхности пластины. Иначе говоря, процесс выравнивания температуры в теле происходит существенно интенсивнее, чем отвод теплоты с поверхности. Остывание лимитирует внешнее термическое сопротивление 1/α – внешняя задача.

Из уравнения (12.20) для этого случая получают следующие уравнения для расчета безразмерной температуры:

На оси, при Х = 0 Θ_Х=0 = exp (-Bi· Fo); (12.22)

На поверхности, при Х = 1 Θ_Х=1 = cos () · exp (-Bi· Fo); (12.23)

3) Число Bi находится в пределах 0,1 ≤ Bi < 100. Температурные кривые будут выглядеть как на рис. 12.4. В этом случае интенсивность процесса охлаждения будет определяться как внутренним, так и внешним термическим сопротивлением.

Дата добавления: 2015-08-21