Неограниченная пластина

t,^oC

Находится аналитическое решение сформулированной выше задачи в одномерном варианте, т.е. требуется найти уравнение температурного поля вида: t = f (x,t).

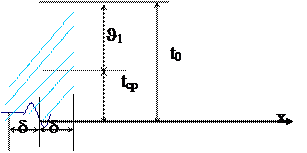
Рисунок 12.2 Плоскопараллельная пластина бесконечной длины и высоты

- Рассматривается охлаждение плоскопараллельной пластины, размеры которой в направлении осей 0Z и 0Y бесконечно велики, а толщина равна 2d.

- Пластина помещена в среду с постоянной температурой – t_ср (или ее обозначают t_ж);

- Коэффициент теплоотдачи с обеих сторон пластины имеет одинаковое и постоянное значение (a).

Так как l_y >> 2d и l_z >> 2d, то дифференциальное уравнение (12.2) принимает вид:

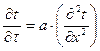; (12.7)

Условия однозначности для рассматриваемого случая:

1) Начальные условия

В начальный момент времени пластина имеет во всех точках постоянную температуру: при t = 0; t_о = const, а превышение температуры пластины над температурой среды (в случае ее охлаждения): J₁ = t_о - t_ср, (начальная избыточная температура).

2) Физические условия

Задан коэффициент температуропроводности материала пластины: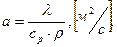

3) Геометрические условия

- d £ х £ +d;

4) Граничные условия III рода при t > 0

(*)

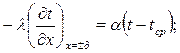Сформулируем поставленную задачу в безразмерных переменных:

Безразмерная температура:

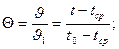(12.8)

J₁= t₀ - t_ср – избыточная температура в начале процесса при t = 0;

J = t - t_ср – текущая избыточная температура при t > 0;

Безразмерная координата:

C= х /d: (12.9)

Подставив эти величины в уравнение (12.7), получим:

(12.10)

где 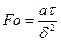- число Фурье – «безразмерное время».

Начальные условия при t = 0;

Fo = 0 Þ Q = 1, так как J = J₁

Граничные условия: при t > 0; Fo > 0 и C = 1 уравнение (*) запишется в виде:

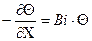; (12.11)

где 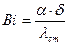Þ критерий Био.

Формулировка этой задачи в безразмерном виде содержит единственный параметр критерий Био.

Критерий – потому, что, составлен из величин, входящих в условия однозначности.

Формально критерий Био сходен с числом Нуссельта 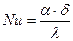. Сходство именно формальное, т.к.:

- использование критерия Био связано с нахождением температурного поля в твердом теле, поэтому в знаменателе – коэффициент теплопроводности твердого тела l_ст. Число Nu связано с температурным полем жидкости – в знаменателе коэффициент теплопроводности жидкости l.

- критерий Био – наперед заданный параметр. Число Nu – искомая величина.

В результате решения составленной в безразмерном виде системы уравнений (12.8, 12.9, 12.10, 12.11) температура поверхности стенки пластины (t_ст) и температура в центральной плоскости пластины (t_ц) определятся из соотношений:

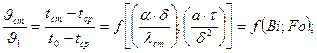(12.12)

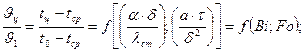(12.13)

J_ст = t_ст – t_cр, - текущая избыточная температура стенки пластины по сравнению с температурой среды, ^оС;

J_ц = t_ц – t_cр, - текущая избыточная температура центра пластины по сравнению с температурой среды, ^оС;

Эти выражения справедливы и при нагреве и при остывании пластины, т.е и при t_о < t_cр, и при t_о > t_cр.

Количество теплоты, которое отдает (или воспринимает) пластина в окружающую среду за время t, должно равняться изменению её внутренней энергии за период её охлаждения (или нагревания).

Начальная внутренняя энергия пластины, отсчитанная от её же внутренней энергии при температуре среды, окружающей стенку, как от нуля, равна:

Q_o = 2d×F×c_p×r×(t₀ - t_cp) = 2d×F×c_p×r×J₁, Дж (12.14)

F – площадь боковой поверхности пластины, м²;

Q_о – «избыточная» внутренняя энергия пластины, (в случае охлаждения).

Введение этой величины необходимо для приведения теплового потока к безразмерному виду.

Количество теплоты, выделившееся в окружающую среду за время τ:

Q_τ = 2d×F×c_p×r×(t₀ - t_cт), Дж (12.15)

t_cт – средняя температура стенки по истечении времени τ.

Количество теплоты, выделяющееся при охлаждении пластины за время τ, определится из выражения:

(12.16)

Зависимости 12.12, 12.13 и 12.16 даются в виде графиков (номограмм) и таблиц, причем последние точнее.

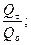
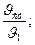
Как правило, начальная температура тела t_о и температура среды t_cр – заданы. Вначале вычисляют Fo и Bi, по которым определяют: 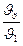, а затем t_cт, t_ц и Q_τ.

Как было показано выше уравнения (12.9), (12.10) и (12.11) формулируют задачу нестационарной теплопроводности в безразмерном виде.

Если рассматривать два процесса нестационарной теплопроводности с одинаковыми числами Bi, т.е Bi₁ = Bi₂ то, согласно третьей теореме подобия, эти процессы подобны. Это значит, что в сходственных точках, т.е. при C₁ = C₂; Fo₁ = Fo₂ безразмерные температуры будут численно равны Θ₁ = Θ₂.

Следовательно, произведя один расчет температурного поля в безразмерном виде, мы получим результат справедливый для всего класса подобных явлений, которые могут различаться размерными параметрами: а, α, λ, δ, t₀, t_cp.

Например, класс явлений нестационарной теплопроводности при охлаждении (нагревании) плоско-параллельной пластины:

Θ = f (Fo, Bi, C), т.к. Bi – задано, то: Θ = f (Fo, C).

Дата добавления: 2015-08-21