Расчет температурного поля при нестационарной теплопроводности для случая охлаждения плоско-параллельной пластины

И для определения температур в центре и на поверхностях пластины, и для определения теплоты, выделившейся при охлаждении пластины, необходимо знать распределение температур в ее теле, т.е. уравнение температурного поля.

Для аналитического решения задачи, включающей уравнение (12.7), и краевые условия используют метод разделения переменных, т.е. ищут решение в виде:

J= f(τ, х) = f₁ (х) · f₂ (τ), (12.17)

где f₁ – зависит только от координаты х,

f₂ – зависит только от τ.

После целого ряда математических преобразований получают тригонометрическое уравнение вида:

, (12.18)

где μ = κ·δ, а к – некоторая постоянная, полученная в ходе преобразований.

Из анализа этого тригонометрического уравнения следует, что при каждом значении Bi существует бесконечное множество решений. Наиболее просто уравнение (12.18) решается графическим способом.

Обозначим левую часть уравнения через у ₁ = , а правую через у ₂ = . Пересечение котангенсоиды у ₁ с прямой у ₂ дает значение корней уравнения (12.18), т.е. μ.

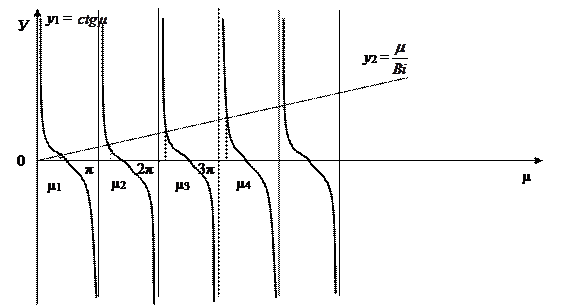
Рисунок 12.3 К решению уравнения (12.18)

Из рисунка 12.3 следует, что μ₁ < μ₂ < μ₃ < μ₄ < …

Важно отметить, что каждому числу Bi соответствует своя совокупность корней уравнения (12.18). Первые четыре корня уравнения μ₁, μ₂ , μ₃, μ₄ приводятся в справочной литературе в табличной форме для различных значений числа Bi (от 0 до ∞).

При Bi → ∞ прямая у ₂ = 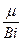совпадает с осью абсцисс и корни уравнения будут равны:

что μ₁ = π/2; μ₂ = 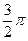; μ₃ = 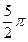; μ_n = .

При Bi → 0 прямая у ₂ = 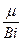совпадает с осью ординат и тангенс угла наклона прямой стремится к бесконечности, при этом корни уравнения (12.18) равны:

μ₁ =0; μ₂ = π; μ₃ = 2π; μ_n = , где n = 1,2,3….

Для других конечных значений числа Bi μ_n имеют промежуточные значения. Следовательно, каждому найденному значению корня μ будет соответствовать свое частное распределение температуры.

Общее решение дифференциального уравнения (12.7) для текущей избыточной температуры J = t - t_ср при t > 0 представляют в виде суммы бесконечного ряда:

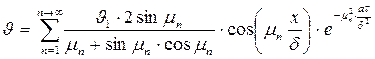(12.19)

Уравнению температурного поля (12.19) целесообразно придать безразмерную форму. Для этого следует разделить обе части уравнения на J₁ – избыточную температуру в начале процесса при t = 0.

Входящие в уравнение (12.19) величины - число Фурье и C= х d, являются безразмерными. С учетом этого уравнение температурного поля для бесконечной пластины в безразмерной форме примет вид:

(12.20)

Анализ полученного решения, уравнения (12.20) показывает, что т.к. μ₁; μ_{2 …}; μ_n представляет собой ряд возрастающих чисел, то чем больше μ, тем меньше роль последующего ряда по сравнению с предыдущим. Кроме того, чем больше , тем члены ряда будут убывать быстрее. Многочисленные исследования показали, что уже при Fo ≥ 0,3, ряд (формула 12.20) становится настолько быстросходящимся, что температурное поле достаточно точно описывается первым членом ряда, ошибка не превышает 1 %.

Дата добавления: 2015-08-21