Определение количества теплоты, отданного пластиной в процессе охлаждения

Из уравнения (12.15) следует, что расчет количества теплоты отданного (или воспринятого) пластиной сводится к определению средней температуры пластины в интересующий нас момент времени.

Внутренняя энергия пластины, отсчитанная от температуры среды, как от нуля в начальный момент времени (при τ = 0):

Q_o = 2d×F×c_p×r×(t₀ - t_cp),

А в момент времени τ₁:

Q₁ = 2d×F×c_p×r×(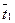 - t_cp). (12.24)

Очевидно, что в окружающую среду выделилось следующее количество теплоты:

Q = Q_o - Q₁= 2d×F×c_p×r×[(t₀ - t_cp) – (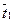 -t_cp)] = 2d×F×c_p×r×(t₀ - t_cp)· =

= Q_o·(1- ); (12.25)

Средняя безразмерная температура для слоя пластины от оси симметрии до плоскости Х найдется, в соответствии с теоремой о среднем, как:

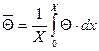(12.26)

Если в это выражение подставить под знак интеграла значение Θ из формулы (12.20) и принять, что Fo ≥ 0,3 и можно ограничиться первым членом ряда, то определится из выражения:

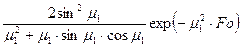= (12.27)

Дата добавления: 2015-08-21