Охлаждение (нагревание) шара

Рассмотрим охлаждение шара в среде с постоянной температурой t_cp и постоянным коэффициентом теплоотдачи α. В начальный момент времени при τ = 0 все точки шара с радиусом r₀ имеют одинаковую температуру t₀. Теплофизические параметры λ, С_р, ρ не зависят от температуры и считаются известными. При заданных условиях температура для любой точки шара будет функцией только времени и безразмерной координаты R = r/r₀.

Также требуется найти распределение температуры внутри шара, т.е. уравнение температурного поля.

Если обозначить текущую избыточную температуру для любой точки шара J = t - t_ср, то дифференциальное уравнение теплопроводности шара в сферических координатах запишется:

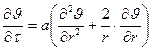(12.35)

Геометрические и физические условия заданы.

Начальные условия: при τ = 0; J₁ = t - t_ср для всех точек шара.

Граничные условия:

На поверхности шара при r = r₀; .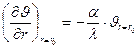

Из условия симметрии задачи в центре шара при r = 0: .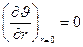

Решая уравнение (12.35) методом разделения переменных и, подчиняя полученное решение начальным и граничным условиям, после ряда преобразований для Fo ≥ 0,3 получим:

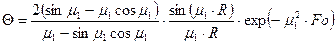(12.36)

Т.к. μ в уравнении (12.36) зависит только от числа Bi, то уравнение температурного поля в общем виде:

Θ = f (Fo, Bi, R).

Для центра шара: Θ_R=0 = f₁ (Fo, Bi) (12.37)

Для поверхности шара: Θ_R=1 = f₂ (Fo, Bi) (12.38)

Функции, определяемые выражениями (12.37) и (12.38) для различных значений Fo и Bi представлены в виде номограмм.

Аналогично, как для пластины и цилиндра начальная избыточная внутренняя энергия шара:

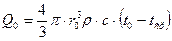(12.39)

Количество теплоты, которое отдается или воспринимается шаром за промежуток времени от τ = 0 до τ₁, также можно определить по номограмме, которая построена по функции вида: Q/Q₀ = f (Bi, Fo)/

Дата добавления: 2015-08-21