Постановка задачи

ТМО-12 ТЕПЛОПРОВОДНОСТЬ ПРИ НЕСТАЦИОНАРНОМ РЕЖИМЕ

Постановка задачи

Рассмотренные ранее процессы стационарной теплопроводности являются по сути дела предельными тепловыми состояниями тел, наступающими при постоянных граничных условиях через продолжительный промежуток времени. Стационарному состоянию предшествует период, в течение которого распределение температур в теле изменяется во времени. (Пример: включение системы отопления, прогрев ограждающей конструкции при t_н = const, а затем стационарный процесс теплопередачи через ограждение при t_н = const и t_в = const).

Если температурное поле нестационарное (изменяется во времени), то тепловые процессы, протекающие в таких условиях, называются нестационарными.

В общем случае уравнение трехмерного нестационарного температурного поля:

t = f (x,y,z,t) (12.1)

Нахождение конкретного вида уравнения (12.1) и является основной задачей нестационарной теплопроводности – поскольку определить изменения теплового потока во времени и пространстве, возможно только зная закон изменения температурного поля.

Уметь определять закономерности изменения температурного поля и теплового потока во времени и пространстве при нестационарной теплопроводности необходимо для решения практических инженерных задач в самых различных отраслях техники:

- при нагреве и охлаждении металлических заготовок;

- при прокаливании твердых тел в производстве стекла, кирпича, керамических изделий;

- при вулканизации резины;

- в отоплении, вентиляции, кондиционировании воздуха, теплогенерирующих установках и т.д.

Пример: ограждения зданий испытывают, изменяющееся во времени (иногда резко), тепловое воздействие, как со стороны наружного воздуха, так и со стороны помещения. В массиве ограждения осуществляется процесс нестационарной теплопроводности.

Формулировка задачи нестационарной теплопроводности включает:

- основное уравнение теплопроводности

(12.2)

- краевые условия (условия однозначности)

1) начальные условия – задают значение искомой функции t в начальный момент времени, т.е. распределение температур в теле и температуру окружающей среды в начальный момент времени;

2) физические условия – теплофизические параметры тела:

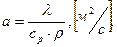
3) геометрические – геометрические размеры тела;

4) граничные - граничные условия формулируют в виде граничных условий III рода, часто встречающихся на практике при постоянной температуре окружающей среды, и одинаковом коэффициенте теплоотдачи по всей поверхности рассматриваемого тела.

y

Для определенности рассмотрим в качестве тела, в котором необходимо найти температурное поле прямоугольный параллелепипед с размерами граней 2d; 2l_y; 2l_z.

z

x

l_z

l_z

l_y

l_y

d

d

Рисунок 12.1 Формулировка задачи нестационарной теплопроводности для прямоугольного параллелепипеда

Если начало декартовой системы координат расположить в центре симметрии параллелепипеда, то:

1) начальные условия запишутся в виде:

при t = 0, t₀ = f (x,y,z,); (12.3)

2) физические - заданы l, С_р, r тела; (12.4)

3) геометрические - - d £ х £ + d; - l_y £ у £ +l_y; - l_z £ z £ +l_z; (12.5)

4) граничные условия III рода при t > 0, одинаковом коэффициенте теплоотдачи a по всей поверхности тела и постоянной заданной величине температуры окружающей среды – t_ср можно записать в виде:

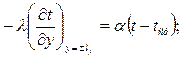(12.6)

Температура в каждом из трех приведенных уравнений берется на соответствующей грани параллелепипеда, (например: для первого уравнения на двух гранях нормальных к оси х и отстоящих от 0 на расстоянии d).

Задача процесса нестационарной теплопроводности в теле приведенного параллелепипеда сформулирована в уравнениях – 2, 3, 4, 5, 6.

Её можно решить аналитически, т.е. путем алгебраических преобразований, дифференцирования, интегрирования и т.д. В результате может быть получена формула для расчета температурного поля: t = f (x,y,z,t).

В большинстве практически важных случаев аналитического решения сформулированной системы уравнений получить нельзя, поэтому стараются упростить задачу и применяют численные методы, которые для задач теплопроводности проработаны весьма фундаментально.

Дата добавления: 2015-08-21