Охлаждение (нагревание) бесконечно длинного цилиндра

12.6.1 Постановка задачи

Цилиндр, радиусом r₀ отдает теплоту окружающей среде через свою боковую поверхность; λ, С_р, ρ не зависят от температуры и считаются известными, заданными; коэффициент теплоотдачи α во всех точках поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура среды t_cp постоянна.

Отсчет температуры цилиндра, как и для пластины, будем вести от температуры среды. В начальный момент времени избыточная температура цилиндра составит: J₁ = t - t_ср.

При этих условиях уравнение теплопроводности для цилиндра:

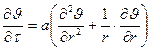(12.28)

Начальные условия: при τ = 0 J = J₁.

Граничные условия: при τ > 0 и R = 0;

R = 1; .

Задачу, сформулированную уравнением (12.28) и условиями однозначности решают методом разделения переменных и в результате математических преобразований получают решение в виде:

(12.29)

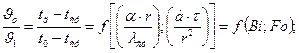(12.30)

Величины и определяют по таблицам или номограммам.

12.6.2 Определение количества теплоты, отданного цилиндром

Так же как и для пластины, количество теплоты Q_o, Дж, которое отдается или воспринимается поверхностью цилиндра за время от τ = 0 до τ = ∞, должно равняться изменению внутренней энергии цилиндра за период его полного охлаждения:

Q_o = π·r₀²× l ×c_p×r×(t₀ - t_cp) (12.31)

За любой промежуток времени от τ = 0 до τ₁ внутренняя энергия цилиндра изменится на величину: Q = Q_o·(1- );

где, как и для пластины = .

Средняя безразмерная температура цилиндра определится из уравнения:

(12.32)

Безразмерная координата R = r/r₀ изменяется от 0 до1.

Если в это уравнение подставить значение Θ для цилиндра (формула для цилиндра получена тем же методом, как и формула (12.20) для пластины) и проинтегрировать в указанных пределах, то получим:

. (12.33)

Для случая Fo ≥ 0,3 (в некоторых источниках 0,25), можно ограничиться первым членом ряда:

. (12.34)

Дата добавления: 2015-08-21