Вывод уравнения плоскости, проходящей через точку, перпендикулярно вектору, и проходящей через 3 точки.

Требуется составить уравнение плоскости, проходящей через точку перпендикулярно вектору

Выберем в пространстве произвольную точку . Обозначим — радиус-векторы точек и Точка принадлежит заданной плоскости тогда и только тогда, когда векторы и перпендикулярны (рис.4.8,б). Условие ортогональности запишем при помощи скалярного произведения:

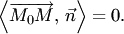
Учитывая, что , получаем векторное уравнение плоскости:

Пусть в координатном пространстве заданы три точки не лежащие на одной прямой (рис.4.17). Требуется составить уравнение плоскости, проходящей через заданные точки.

Точка принадлежит плоскости, проходящей через точки 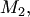тогда и только тогда, когда ее радиус-вектор удовлетворяет условию:

где - некоторые действительные числа (параметры). Это уравнение, а также его координатную форму

будем называть аффинным уравнением плоскости, проходящей через точки

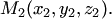
Используя векторы

и

в качестве направляющих векторов плоскости, составим уравнение вида (4.18):
которое называется уравнением плоскости, проходящей через три заданные точки.

Дата добавления: 2015-08-21