Параметрические и канонические уравнения прямой.

Определение. Любой ненулевой вектор, коллинеарный данной прямой называется ее направляющим вектором.

Пусть L – произвольная прямая и – ее произвольная, но фиксированная точка, О – начало координат, – произвольная (текущая) точка прямой L, – радиус вектор точки , – радиус вектор текущей точки М, 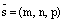– произвольный направляющий вектор прямой L.

рис.5.

Теорема. Следующая система уравнений является параметрическими уравнениями прямой:

, , (7)

где – координаты произвольной фиксированной точки данной прямой, – соответствующие координаты произвольного направляющего вектора данной прямой, t – параметр.

Доказательство. В соответствии с определением уравнения любого множества точек координатного пространства, мы должны доказать, что уравнениям (7) удовлетворяют все точки прямой L и, с другой стороны, не удовлетворяют координаты точки не лежащей на прямой.

Пусть произвольная точка . Тогда векторы и являются по определению коллинеарными и по теореме о коллинеарности двух векторов следует, что один из них линейно выражается через другой, т.е. найдется такое число , что . Из равенства векторов и следует равенство их координат:

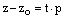, , , ч.т.д.

Обратно, пусть точка . Тогда и по теореме о коллинеарности векторов ни один из них не может быть линейно выражен через другой, т.е. и хотя бы одно из равенств (7) не выполняется. Таким образом, уравнениям (7) удовлетворяют координатытолько тех точек, которые лежат на прямой L и только они, ч.т.д.

Теорема доказана.

Следствие. Следующая система уравнений является уравнениями прямой:

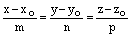. (8)

Доказательство. Выразив параметр t из уравнений (7), получаем:

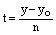, , , (9)

откуда и следуют уравнения (8). Ясно, что системы уравнений (7) и (8) равносильны, т.е. их множества решений совпадают и система (8), так же как и система (7), являются уравнениями прямой, ч.т.д.

Следствие доказано.

Определение. Уравнения (8) называются каноническими уравнениями прямой.

8.

Дата добавления: 2015-08-21