Читайте также:
|
Теорема 1.6 (формула вычисления скалярного произведения в ортонормированном базисе). В ортонормированном базисе скалярное произведение векторов равно сумме произведений одноименных координат векторов:
— если векторы 
и 
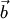относительно ортонормированного базиса на плоскости имеют координаты 
и 
соответственно, то скалярное произведение этих векторов вычисляется по формуле
| (1.9) |
— если векторы относительно ортонормированного базиса в пространстве имеют координаты 
и 
соответственно, то скалярное произведение этих векторов вычисляется по формуле
| (1.10) |
Докажем формулу (1.10). Пусть в пространстве задан ортонормированный (стандартный) базис 
. Скалярные произведения базисных векторов находятся по определению:
| (1.11) |
Используя линейность скалярного произведения по любому множителю, для векторов 
и 
получаем:
Учитывая (1.11), из девяти слагаемых только три отличны от нуля, поэтому
что и требовалось доказать.
Дата добавления: 2015-08-21; просмотров: 298 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение и свойства скалярного произведения векторов | | | Определение и свойства векторного произведения векторов |