Определение и свойства векторного произведения векторов

Векторным произведением векторов и называется вектор , который определяется следующими условиями:

1) Его модуль равен где - угол между векторами и .

2) Вектор перпендикулярен к плоскости, определяемой перемножаемыми векторами и .

3) Вектор направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы и , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок).

Векторное произведение векторов и обозначается символом :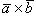

(25)

или

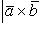
(26)

Основные свойства векторного произведения:

1) Векторное произведение 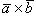равно нулю, если векторы и коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):

Векторное произведение не обладает свойством переместительности.

Дата добавления: 2015-08-21