Решение линейных систем по формулам Крамера. Исследование линейных систем.

Системы двух линейных уравнений с двумя неизвестными имеют вид:

где a, b, c, d, e, f – заданные числа; x, y – неизвестные. Числа a, b, d, e – коэффициенты при неизвестных; c, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами.

Правило Крамера. Используя определители, можно переписать формулы (3):

Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными.

П р и м е р. Решить систему уравнений

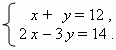
используя правило Крамера.

Р е ш е н и е. Здесь a = 1, b = 1, c = 12, d = 2, e = – 3, f = 14.

Исследование решений системы двух линейных уравнений с двумя неизвестными, показывает, что в зависимости от коэффициентов уравнений возможны три различных случая:

1) коэффициенты при неизвестных не пропорциональны: a: d ≠ b: e,

в этом случае система линейных уравнений имеет единственное решение, получаемое по формулам (4);

2) все коэффициенты уравнений пропорциональны: a: d = b: e = c: f,

в этом случае система линейных уравнений имеет бесконечное множество решений, так как здесь мы имеем фактически одноуравнение вместо двух.

Дата добавления: 2015-08-21