Уравнение прямой, проходящей через точку, перпендикулярно заданному вектору

Пусть даны вектор 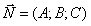, перпендикулярный плоскости Q и точка М₁ (x₁; y₁; z₁), которая лежит на этой плоскости. Представим вектор N направленным отрезком MP. Выберем на плоскости Q произвольную точку M(x; y; z) и назовем ее текущей точкой, а ее координаты (x; y; z) – текущими координатами.

Рассмотрим вектор . Его координаты равны

(x – x₁); (y – y₁); (z – z₁).

Рис. 1.26. Плоскость

Поскольку вектор N перпендикулярен плоскости Q, то он перпендикулярен любой линии, находящейся в этой плоскости. Т.е. вектора N и перпендикулярны, следовательно, их скалярное произведение равно нулю.

(1-61)

Выразим данное скалярное произведение через координаты векторов

A(x – x₁) + B(y – y₁) + C(z – z₁) = 0, (1-62)

где А, В, С – координаты нормального вектора,

x₁, y₁, z₁ – координаты данной точки,

x, y, z – текущие координаты точек поверхности.

Равенство (1-62) называется уравнением плоскости, походящей через данную точку, перпендикулярно данному вектору.

После преобразования (1-62) получаем

Ax + By + Cz + D = 0 (1-63)

Дата добавления: 2015-08-21