Производная

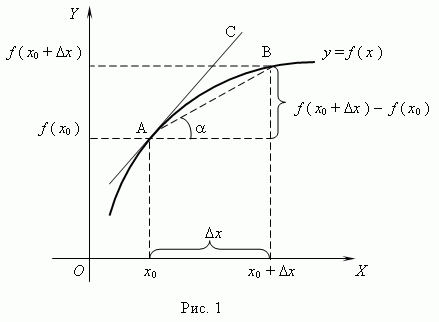Геометрический смысл производной. Рассмотрим график функции y = f (x):

Из рис.1 видно, что для любых двух точек A и B графика функции:

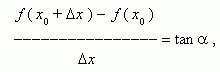
где - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точкуB, то 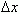неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Уравнение касательной. Выведем уравнение касательной к графику функции в точке A (x ₀, f (x ₀)). В общем случае уравнение прямой с угловым коэффициентом f ’(x ₀) имеет вид:

y = f ’(x ₀) · x + b.

Чтобы найти b,воспользуемся тем, что касательная проходит через точку A:

f (x ₀) = f ’(x ₀) · x ₀ + b,

отсюда, b = f (x ₀) – f ’(x ₀) · x ₀, и подставляя это выражение вместо b, мы получим уравнение касательной:

y = f (x ₀) + f ’(x ₀) · (x – x ₀).

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке 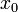, а функция g имеет производную в точке 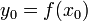, то сложная функция h(x) = g(f(x)) также имеет производную в точке .

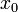Неопределенный интеграл:

1.Первообразная. Функция F(х) называется первообразной для функции f (х) на промежутке X, если для любого х из Х выполняется равенство F'(x)=f(x)

Т.7.13 (Если F(х)-первообразная для функции f(х) на промежутке X, то у функции f(x) бесконечно много первообразных, и все эти первообразные имеют вид F (x)+С, где С - произвольная постоянная (основное свойство первообразной).

2.Таблица первообразных. Учитывая, что отыскание первообразной есть операция, обратная дифференцированию, и отталкиваясь от таблицы производных, получаем следующую таблицу первообразных (для простоты в таблице приведена одна первообразная F(х), а не общий вид первообразных F(х) + С:

Функция	Первообразная	Функция	Первообразная

3.Правила вычисления первообразных:
1. Если F(х)-первообразная для f(x), а Н(х)-первообразная для h(х), то F(х)+Н(х)- первообразная для f(х)+h(х). Иными словами, первообразная суммы равна сумме первообразных.
2. Если F(х) - первообразная для f(х) и k - постоянная, то kF(х) - первообразная для kf(х). Иными словами, постоянный множитель можно вынести за знак первообразной.
3. Если F(х) - первообразная для f(х) и k, b- постоянные, причем k≠0, то F(kx+b) - первообразная для f (kх+b).

Неопределенным интегралом 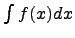называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е. или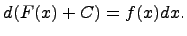

Основные свойства

1.

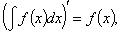
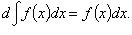
2.

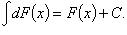
3. Если 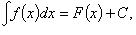то

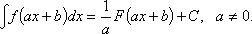
4.

Дата добавления: 2015-09-03