Линейная комбинация векторов

Базисом на плоскости называются два любых неколлинеарных вектора

Базисом в пространстве называются 3 любых некомпланарных вектора

Если базисные векторы взаимно перпендикулярны, то базис называется ортогональным. Если базисные векторы имеют единичную длину, то такой базис называется ортонормированным. Исключительное удобство этого базиса заключается в том, что координатами любого вектора в базисе i, j, k являются проекции этого вектора на координатные оси

Выражение длины вектора через его координаты:

Скалярное произведение векторов: Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

1. Свойства: свойство коммутативности скалярного произведения ;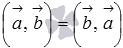

2. свойство дистрибутивност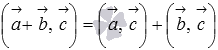и или ;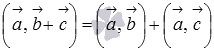

3. сочетательное свойство 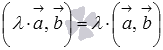или , где 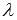- произвольное действительное число;

4. скалярный квадрат вектора всегда не отрицателен 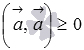, причем 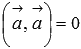тогда и только тогда, когда вектор 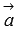нулевой.

Косинус угла между векторами:

Условие перпендикулярности векторов: Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.

Прямая на плоскости: Общее уравнение Ax + By + C (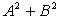 > 0)

Уравнение 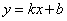называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением 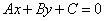, то ее угловой коэффициент определяется по формуле .

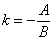Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны:

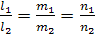– условие параллельности прямых.

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:

– условие перпендикулярности прямых.

Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

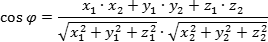
Уравнение прямой, проходящей через две точки: A (x ₁, y ₁) и B (x ₂, y ₂), записывается так: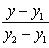

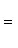
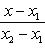
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

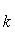
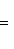
Дата добавления: 2015-09-03