Читайте также:
|
Простейшие задачи, в которых нужно проинтегрировать элементарные функции, решаются при помощи таблицы первообразных. В более сложных случаях нужно знать ряд приемов, сводящих в конечном итоге вычисляемый интеграл к интегралам от табличных функций. Одним из таких приемов является метод замены переменного.
Пусть определены дифференцируемые функции f (x) и g (t), а также сложная функция g (f (x)). Пусть 
Тогда 
Это означает, что
|
Иногда, вычисляя интеграл 
полезно перейти к новой переменной. Пусть x = g (t) монотонная дифференцируемая функция, 
– обратная ей функция. Тогда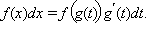 
Обозначая 
получим f (x) dx = u (t) dt. Если 
то
|
Этот метод называется методом подстановки.
Пусть функции u (x) и v (x) имеют непрерывные на D производные. Тогда
|
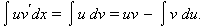
Функция uv имеет непрерывную производную на D, и 
Интегрируя обе части этого равенства, получим 
Относя константу интегрирования к интегралу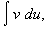 
получаем доказываемую формулу.
Эта формула описывает метод интегрирования по частям. Она сводит вычисление интеграла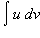 
к вычислению интеграла 
Дата добавления: 2015-09-03; просмотров: 64 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Производная | | | Определенный интеграл: Если функция является первообразной для на отрезке , то число равное разности называется определённым интегралом от функции на отрезке и обозначается |