Линейная алгебра

Задачи к зачету и экзамену

I семестр.

Линейная алгебра

1. Найти общее и частное решение системы линейных уравнений

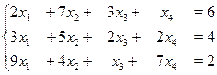
Решение. При помощи элементарных преобразований приведем расширенную матрицу к ступенчатому виду.

На пересечении первых двух строк и первых двух столбцов находится матрица треугольного вида. Поэтому объявим зависимыми неизвестными, а – свободными. Запишем систему линейных уравнений, соответствующую полученной ступенчатой матрице

Перенесем слагаемые, содержащие свободные неизвестные вправо

Выразим через

Получено общее решение системы линейных уравнений. Пусть, например, 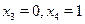, тогда, подставляя эти значения в формулы общего решения, получим , т.е. 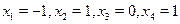– частное решение нашей системы линейных уравнений.

2. Решить систему линейных уравнений:

Ответ: .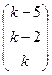

3). Используя свойства определителей, вычислить:

.

Решение:

Сведем задачу вычисления определителя четвертого порядка к задаче вычисления определителей более низких порядков, при этом используя свойство:

определитель ∆ порядка n равен сумме произведений элементов некоторой строки а_ij (или столбца) на их алгебраические дополнения А_ij:

.

Определитель не изменится, если к каждому элементу какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же отличное от нуля число. Учитывая это, получим в первой строке три нуля (два уже есть по условию):

.

Разложим определитель по элементам первой строки:

Ответ: ∆ = – 20.

4. Найти произведение матриц:

и .

Решение:

Размерности матриц А и В:

А: (3х2), В: (2х2)

удовлетворяют определению операции произведения матриц (количество столбцов матрицы А равно количеству строк матрицы В (2 = 2)).

Тогда размер матрицы С=АВ: (3х2). Т. е.:

.

Найдем ее элементы по формуле:

,

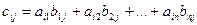т.е. для нахождения элемента с_ij умножим элементы i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В. Получим:

Ответ: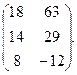

5) Определить, имеет ли данная матрица обратную, найти обратную матрицу к данной .

Решение:

Вычисляем определитель матрицы:

.

|A| ¹ 0 Þ матрица имеет обратную ей матрицу. Находим алгебраические дополнения элементов этого определителя:

Таким образом: .

Ответ: .

Дата добавления: 2015-08-21