Алгебра Диофанта

Греческий математик Диофант (III век нашей эры) был последним великим математиком античности. До него уравнения решались в словесной либо в геометрической форме. Он впервые использовал в алгебре буквенную символику. Но введенные им буквенные обозначения были сокращениями соответствующих математических терминов, а не алгебраическими символами в нашем понимании. Тем не менее новшества Диофанта имели революционный характер. Он ввел обозначения неизвестной величины, ее первых шести положительных и отрицательных степеней, отрицательные числа, знак “минус” и знак “равенство”. Благодаря этому Диофанту удалось получить ряд важных результатов. Он даже сумел предвосхитить подстановки Эйлера [3, 4]. Однако современному читателю символика Диофанта кажется странной, запутанной и очень непривычной.

Попробуем запастись терпением и совершим небольшую прогулку по джунглям диофантовой алгебры, ограничившись одним-единствен­ным вопросом: как Диофант записывал уравнения?

Прежде всего, попытаемся выяснить: как будут выглядеть наши современные знаки

,

если их перевести на язык Диофанта? Ответ дает табл. 8.

Таблица 8

Современная алгебра	Алгебра Диофанта
Обозначение	Как читается	Обозначение	Как читается
x	Неизвестная величина	ζ	Число
x 2	Икс квадрат	Δν	Квадрат
x 3	Икс куб	Κν	Куб
x 4	Икс в четвертой степени	ΔDν	Квадратоквадрат
x 5	Икс в пятой степени	DΚν	Квадратокуб
x 6	Икс в шестой степени	ΚΚν	Кубокуб
=	Равно	ι	Равно
–	Минус		Недостаток
+	Плюс	Плюс у Диофанта отсутствует. Слагаемые пишутся подряд

Таблица 9

Единицы	Десятки	Сотни	Тысячи
Совре­менная запись	Греческая запись	Совре­менная запись	Греческая запись	Совре­менная запись	Греческая запись	Совре­менная запись	Греческая запись
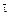
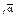
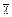
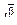
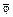
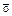
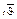
Примечание: в греческой системе счисления нуль отсутствует.

Для обозначения чисел Диофант использует общепринятую у греков символику [5] (табл. 9).

Греческие числа образуют непозиционную десятичную систему: как , так и может значить только 14. Отсутствие позиционной сис­темы вносит большие когнитивные затруднения: задача 4 × 10 = 40 (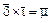) у греков не имеет ничего общего с “родственной” задачей
4 × 100 = 400 (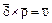). По этому поводу немецкий психолог Фридхарт Кликс восклицает: “Насколько проще метод нашей позиционной системы, насколько меньше затрат при решении одинаковых задач!” [5].

Каждый член уравнения Диофант пишет так: сначала указывается степень неизвестного, потом числовой коэффициент; перед отрицательными членами ставится знак недостатка (по-нашему, минус), перед положительным — ничего (плюсом Диофант не пользуется) (табл. 10).

При записи свободного члена уравнения Диофант сначала ставит символ М° (признак свободного члена), а затем его числовое значение (табл. 11).

Таблица 10

Запись членов уравнения
Современная	У Диофанта	Современная	У Диофанта
x
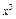
2 x
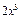
3 x

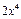
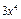
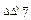
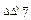
Таблица 11

Запись свободного члена
Современная	У Диофанта
	У греков нуля нет

С учетом сказанного приведем несколько примеров записи уравнений в символике Диофанта. Обратите внимание: чтобы избавиться от нуля, во втором и третьем примерах Диофанту пришлось перенести свободный член в правую часть уравнения (табл. 12).

Таблица 12

Дата добавления: 2015-08-21