Алгебраїчні і трансцендентні числа. Будова простого алгебраїчного розширення поля

Питання для самоконтролю:

1) Яке число називається алгебраїчним відносно поля ?
А яке трансцендентним?

2) Чи існує незвідний зведений многочлен , коренем якого є алгебраїчне число 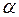відносно поля ? Який його степінь? Як він називається? Скільки таких многочленів існує?

3) Яке поле називається простим алгебраїчним (трансцендентним) розширенням поля ?

4) З яких чисел складається поле , утворене з поля приєднанням кореня α, незвідного у полі многочлена -го степеня ?

5) З яких чисел складається просте алгебраїчне розширення Р(α) поля , якщо α – корінь многочлена і ?

6) Яке розширення поля називається квадратичним?

7) Розширення поля називається скінченим, якщо …

8) Яка степінь будь-якого квадратичного розширення?

9) Яке розширення є складним розширенням поля ?

10) Якщо всі елементи поля є алгебраїчними відносно поля , то розширення називається …

Задачі

1) Довести, що число a є алгебраїчним і знайти його мінімальний многочлен:

2) Довести, що числа і алгебраїчні. Знайти степінь числа .

3) Довести безпосередньо, що число 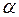є алгебраїчним, і знайти многочлен над Q (не обов’язково мінімальний), коренем
якого є :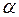

4) Для даного числа 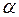, алгебраїчного над Q, знайти алгебраїчно спряжене до нього (над Q) число:

5) Чи міститься в полі число ? В полі
число ?

6) Знайти алгебраїчне число, приєднанням якого до Q поля можна дістати складне алгебраїчне розширення:

де - прості числа,

,

.

7) Нехай 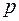і - натуральні числа, причому і - не цілі. Довести, що .

8) Знайти вираження для кожного з чисел і через
+ :

Дата добавления: 2015-08-21