
Читайте также:
|
1) Чи є многочленом від змінної  чи
чи  вираз:
вираз:
а)  ;
;
б) 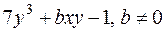 ;
;
в)  ;
;
г)  .
.
2) Який степінь має многочлен  :
:
а) 3;
б) 4;
в) 8;
г) 7.
3) Канонічною формою многочлена  називається такий запис:
називається такий запис:
а) коли його члени впорядковані в довільному порядку;
б) коли його члени впорядковані за спаданням степеня  ;
;
в) коли його члени впорядковані за зростанням степеня  ;
;
г) коли його члени впорядковані за спаданням значення
коефіцієнта.
4) Які з многочленів записані в канонічній формі:
а)  над полем
над полем  ;
;
б)  над полем
над полем  ;
;
в)  над кільцем
над кільцем  ;
;
г)  над полем
над полем 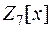 .
.
5) Допишіть нерівність:  …
…
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
6) При яких  та
та 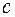 многочлен з кільця
многочлен з кільця  рівні між собою:
рівні між собою:  та
та 
а) 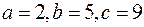 ;
;
б) 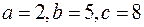 ;
;
в)  ;
;
г)  .
.
7) У кільці  многочлени
многочлени  і
і  …, якщо вони відрізняються лише множником, який є відмінною від нуля константою.
…, якщо вони відрізняються лише множником, який є відмінною від нуля константою.
а) незвідні;
б) асоційовані;
в) подібні;
г) звідні.
8) Знайти суму коефіцієнтів многочлена  з кільця
з кільця  :
:
а) -5;
б) 24;
в) 0;
г) -25.
9) Як називається многочлен  у виразі
у виразі 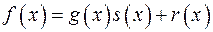 :
:
а) ділене;
б) частка;
в) остача;
г) дільник.
10) Як називається вираз виду  :
:
а) лінійний запис НСД;
б) лінійний запис НСК;
в) лінійне представлення НСД;
г) лінійне представлення НСК.
11) … називається будь-який многочлен  такий, що
такий, що
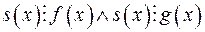 :
:
а) СД;
б) НСК;
в) НСД;
г) СК.
12) Якщо  , то
, то  називається …
називається …
а) СД;
б) НСК;
в) НСД;
г) СК.
13) Многочлен  називається … у полі
називається … у полі  , якщо
, якщо  і в кільці
і в кільці  існують многочлени
існують многочлени  і
і  такі, що
такі, що  =
= 
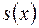 ,
,  і
і  .
.
а) незвідним;
б) асоційованим;
в) симетричним;
г) звідним.
14) Чи вірне твердження: многочлен першого степеня над будь-яким полем  є звідним у кільці
є звідним у кільці  ?
?
а) так;
б) ні;
в) в окремих випадках;
г) можливо.
15) Поле  , де многочлен
, де многочлен  розкладається на лінійні множники називається:
розкладається на лінійні множники називається:
а) канонічним полем;
б) полем розкладу;
в) кратним полем;
г) звідним полем.
16) Якщо  , то многочлени
, то многочлени  і
і  називаються:
називаються:
а) асоційованими;
б) звідними;
в) незвідними;
г) взаємно простими.
17) Число всіх можливих коренів многочлена  степеня
степеня  над
над
полем  …
…
а) дорівнює  ;
;
б) не перевищує  ;
;
в) більше  ;
;
г) менше  .
.
18) Скільки многочленів можуть бути найменшим спільним дільником многочленів  і
і  у кільці
у кільці 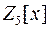 :
:
а) 2;
б) 1;
в) 4;
г) безліч.
19) Скільки многочленів можуть бути найменшим спільним кратним многочленів  і
і  у кільці
у кільці 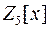 :
:
а) 2;
б) 1;
в) 4;
г) безліч.
20) Раціональний дріб  називається неправильним, якщо …
називається неправильним, якщо …
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
21)  – це …
– це …
а) СД;
б) СК;
в) НСК;
г) НСД.
22) Як називається вираз  :
:
а) канонічний розклад многочлена  ;
;
б) розклад многочлена  на множники;
на множники;
в) лінійне представлення многочлена  ;
;
г) розклад многочлена  на незвідні множники.
на незвідні множники.
23) Елементарним дробом у полі  називається раціональний дріб виду:
називається раціональний дріб виду:
а)  , де
, де  - звідний у полі
- звідний у полі  ,
,  ;
;
б)  , де
, де  - незвідний у полі
- незвідний у полі  ,
,  ,
,  ;
;
в)  , де
, де  - незвідний у полі
- незвідний у полі  ,
,  ,
,  ;
;
г)  , де
, де  - звідний у полі
- звідний у полі  ,
,  ,
,
 ;
;
24) Який з раціональних дробів є елементарним над полем 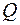 :
:
а)  ;
;
б)  ;
;
в) 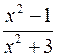 ;
;
г)  .
.
25) Неправильний дріб  над полем
над полем  можна подати як …
можна подати як …
а) суму многочлена і неправильного дробу;
б) різницю многочлена і правильного дробу;
в) суму многочлена і правильного дробу;
г) суму многочленів.
26) Нехай маємо деякий многочлен  . Тоді запис
. Тоді запис  означає:
означає:
а)  - корінь многочлена
- корінь многочлена  ;
;
б) значення многочлена  при
при  .
.
27) Нехай є довільний многочлен  . Що розуміється під записом
. Що розуміється під записом  :
:
а)  - корінь многочлена
- корінь многочлена  ;
;
б) значення многочлена  при
при  .
.
28) Чи вірно, що коли многочлени рівні між собою функціонально, то вони рівні і алгебраїчно?
а) так;
б) ні;
в) практично завжди;
г) майже ніколи.
29) Чи справедливе таке твердження: 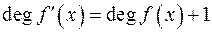 ?
?
а) так;
б) ні;
в) залежно від початкових умов;
г) не знаю.
30) Чи рівносильні алгебраїчне та функціональне тлумачення поняття кореня многочлена над довільною областю цілісності:
а) так;
б) ні;
в) за певних умов;
г) можливо.
31) У кільці 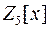 виконуються рівності
виконуються рівності  . Чи не суперечать вони теоремі про єдиність розкладу многочлена на незвідні множники у кільці
. Чи не суперечать вони теоремі про єдиність розкладу многочлена на незвідні множники у кільці 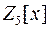 ?
?
а) так;
б) ні;
в) можливо.
32) Вкажіть, які з властивостей подільності многочленів над полем  записані без помилок:
записані без помилок:
а) 








 ;
;
б) 





 (
( ±
±  )
) 
 ;
;
в) 





 Þ
Þ 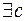
 P [x]
P [x]  = c
= c  ;
;
г) 





 Þ
Þ 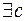
 P [x]
P [x]  = c
= c  .
.
33) Чи вірно записана властивість подільності многочленів над
полем 
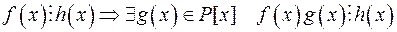 :
:
а) так;
б) ні;
в) можливо;
г) при певному  .
.
34) Довільний многочлен 
 Р[x] ділиться з остачею на будь-який многочлен
Р[x] ділиться з остачею на будь-який многочлен 
 Р[x],
Р[x],  ¹ 0; при цьому частка
¹ 0; при цьому частка 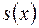 і остача
і остача  належать Р[x] і визначаються однозначно, тобто
належать Р[x] і визначаються однозначно, тобто  , причому …
, причому …
а)  ;
;
б)  ;
;
в) 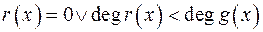 ;
;
г) 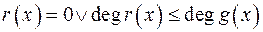 .
.
35) Яке з тверджень неправильне:
а) будь-які многочлени  і
і  мають тривіальні НСД –
мають тривіальні НСД –
дільники одиниці кільця Р[x];
б) будь-які многочлени  і
і  мають тривіальні НСД –
мають тривіальні НСД –
дільники нуля кільця Р[x];
в) будь-які многочлени  і
і  не мають тривіальних НСД.
не мають тривіальних НСД.
36) Чи вірно: якщо 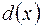 – НСД многочленів
– НСД многочленів  і
і  , то " с
, то " с  0
0  – НСК многочленів
– НСК многочленів  і
і  ?
?
а) так;
б) ні;
в) при певному 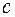 ;
;
г) при певному  .
.
37) Допишіть властивість взаємно простих многочленів 




 (
( ,
,  ) = 1
) = 1 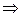 …
…
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
38) Якщо многочлен  є незвідним над полем
є незвідним над полем  , то для будь-якого многочлена
, то для будь-якого многочлена  з кільця
з кільця  …
…
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
39) Якщо многочлен  є незвідним над полем
є незвідним над полем  , то для
, то для  многочлен
многочлен  є …
є …
а) звідним;
б) взаємно простим;
в) асоційованим;
г) незвідним.
40) Допишіть властивість: ( ,
,  ) = 1
) = 1  (
( ,
,  ) = 1
) = 1 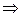 …
…
а)  ;
;
б)  ;
;
в) 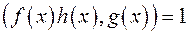 ;
;
г)  .
.
41) Задача 1: остачі від ділення многочлена  з кільця
з кільця  на
на  відповідно дорівнюють
відповідно дорівнюють  та
та  . Знайти остачу від ділення цього многочлена на
. Знайти остачу від ділення цього многочлена на  :
:
а)  ;
;
б)  ;
;
в) 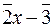 ;
;
42) Задача 2: відокремити кратні множники многочлена  :
:
а) 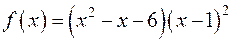 ;
;
б) 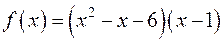 ;
;
в)  .
.
43) Задача 3: дослідити на звідність многочлен  в
в
кільці  :
:
а) звідний;
б) незвідний;
в) не можливо визначити.
44) Задача 4: розкласти дріб  на елементарні дроби над полем
на елементарні дроби над полем 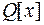 :
:
а)  ;
;
б)  ;
;
в)  .
.
ТЕСТ 2
Дата добавления: 2015-08-21; просмотров: 668 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Алгебраїчні і трансцендентні числа. Будова простого алгебраїчного розширення поля | | | Симетричні многочлени |