Рівняння третього степеня

Питання для самоконтролю:

1) Яке рівняння називається рівнянням третього степеня?

2) Рівняння третього степеня зводиться до рівняння виду за допомогою …

3) Як називається вираз ?

4) Як знайти корені рівняння ?

5) Коли рівняння має один дійсний і два комплексні корені спряжених?

6) Якщо 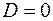, то які корені має рівняння ?

7) Рівняння має три дійсні корені, якщо …

8) U₁ i V₁ – це …

9) З якої умови знаходиться числа U₁ i V₁?

Задачі

1) Звести кубічне рівняння до виду, у якому відсутній доданок з невідомим у другому степені:

2) Розв’язати рівняння:

3) При яких дійсних значеннях рівняння має кратний корінь? Знайти його.

4) Які корені залежно від значення числа має рівняння з дійсними коефіцієнтами ?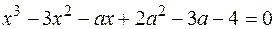

5) Розв’язати рівняння , коли відомо, що серед його коренів є два числа, обернених за абсолютною величиною і протилежних за знаком.

6) Розв’язати рівняння , коли відомо, що добуток двох його коренів дорівнює 1.

7) Розв’язати кубічне рівняння , коли відомо, що його коефіцієнти в порядку спадання степенів утворюють геометричну прогресію з знаменником 2.

Дата добавления: 2015-08-21