Кільце многочленів від n змінних. Розклад многочлена на добуток незвідних множників. Симетричні многочлени

Питання для самоконтролю:

1) Многочленом від 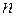змінних над полем називається …

2) Наведіть приклади многочлена від трьох змінних.

3) Що є степенем члена ?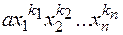

4) Степінь многочлена – це …,
старшим членом многочлена називають …

5) Чому дорівнює степінь добутку двох многочленів?

6) Що означає відношення „бути вищим”?

7) Чи є такий запис многочлена лексикографічним? Відповідь пояснити.

8) Який многочлен від 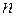змінних називається звідним (незвідним) у полі ?

9) Назвіть властивості незвідних многочленів?

10) Чи можливо подати многочлен 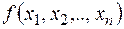не нульового степеня над полем у вигляді добутку незвідних у полі многочленів?

11) Примітивний многочлен – це …

12) Дати означення симетричного многочлена відносно змінних 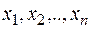многочленна.

13) Сформулювати основну теорему теорії симетричних многочленів.

14) Назвіть властивості симетричних многочленів.

Задачі

1) Знайти канонічну форму таких многочленів: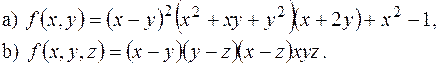

2) Упорядкувати лексикографічно і знайти вищий член многочлена:

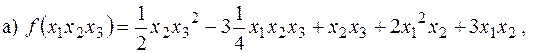
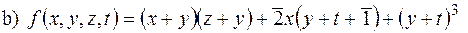з кільця .

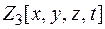3) Застосовуючи заміну розкласти на незвідні у полі множники многочлен 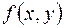, якщо

4) Розкласти на незвідні множники многочлен :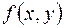

5) Чи є симетричними такі многочлени:

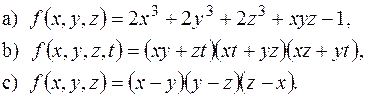
6) Виразити через елементарні симетричні многочлени:

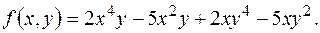
7) Перевірити вірність даної рівності: .

8) Виразити через елементарні симетричні многочлени:

Дата добавления: 2015-08-21