Розділ IV. Многочлени над полем раціональних чисел та алгебраїчні числа

Цілі і раціональні корені многочлена з цілими коефіцієнтами. Критерій незвідності Ейзенштейна

Питання для самоконтролю:

1) Число якого виду може бути раціональним коренем многочлена?

2) При якій умові число , де , може бути коренем рівняння з цілими коефіцієнтами?

3) Коли всі раціональні корені є цілими числами і являються дільниками вільного члена?

4) Якщо числа є цілими, то є …

5) Умова звідності многочлена з цілими коефіцієнтами у полі раціональних чисел.

6) Якщо многочлен з раціональними коефіцієнтами, 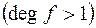має хоч один раціональний корінь , то …

7) Сформулюйте критерій Ейзенштейна незвідності многочлена з цілими коефіцієнтами.

Задачі

1) Розв’язати рівняння:

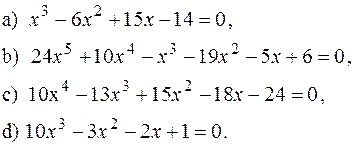
2) Знайти раціональні корені рівняння:

3) Розкласти на незвідні множники дані многочлени або довести їх незвідність:

4) Дослідити на звідність у полі Q такий многочлен: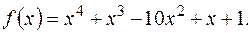

5) Що можна сказати про звідність даного многочлена у
кільці :

6) Користуючись критерієм Ейзенштейна, довести незвідність над полем Q многочленів:

Дата добавления: 2015-08-21