
Читайте также:
|
1) Два члени многочлена, що відрізняються лише коефіцієнтами називаються:
а) взаємно простими;
б) асоційованими;
в) подібними;
г) незвідними.
2) Степенем члена  називається:
називається:
а) добуток 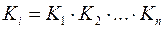 ;
;
б) різниця  ;
;
в) сума 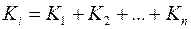 ;
;
г) добуток  .
.
3) Який степінь многочлена  :
:
а) 3;
б) 4;
в) 5;
г) 6.
4) Який „вищий” член многочлена 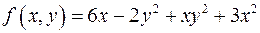 :
:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
5) Який старший член многочлена 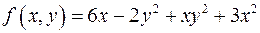 :
:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
6) Якщо всі члени многочлена мають однаковий степінь, то многочлен називається:
а) примітивним;
б) подібним;
в) однорідним;
г) зведеним.
7) Який з многочленів записаний лексикографічно:
а)  ;
;
б)  ;
;
в)  ;
;
г) 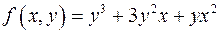 .
.
8) Якщо многочлени 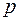 та
та  незвідні у полі
незвідні у полі  і
і 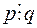 , то вони:
, то вони:
а) примітивні;
б) звідні;
в) асоційовані;
г) прості.
9) Многочлен 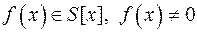 називається …, якщо НСД його коефіцієнтів рівний 1.
називається …, якщо НСД його коефіцієнтів рівний 1.
а) асоційованим;
б) звідним;
в) симетричним;
г) примітивним.
10) Який з цих многочленів симетричний:
а)  ;
;
б) 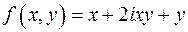 ;
;
в)  ;
;
г) 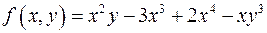 .
.
11) Як виражається через елементарні симетричні многочлени сума  :
:
а) 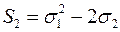 ;
;
б)  ;
;
в) 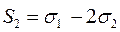 ;
;
г) 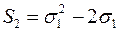 .
.
12) Нехай 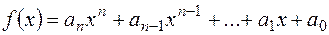 і
і
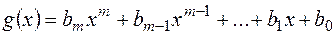 , де
, де 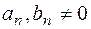 і
і
 - корені
- корені 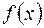 , тоді результант
, тоді результант 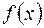 і
і 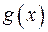
має вигляд:
а) 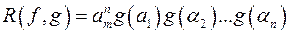 ;
;
б)  ;
;
в) 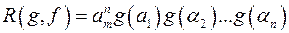 ;
;
г) 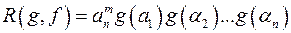 .
.
13) Яке з тверджень вірне:
а)  ;
;
б) 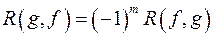 ;
;
в) 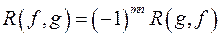 ;
;
г)  .
.
14) Для того, щоб многочлени 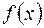 і
і  мали спільний корінь необхідно і достатньо, щоб …
мали спільний корінь необхідно і достатньо, щоб …
а)  ;
;
б) 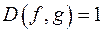 ;
;
в)  ;
;
г)  .
.
15) Дискримінант многочлена це вираз виду:
а) 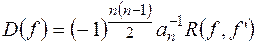 ;
;
б)  ;
;
в) 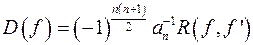 ;
;
г) 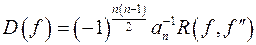 .
.
16) Для того, щоб многочлен 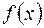 мав кратний корінь необхідно, щоб:
мав кратний корінь необхідно, щоб:
а)  ;
;
б) 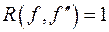 ;
;
в) 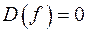 ;
;
г)  .
.
17) Скільки членів може мати канонічна форма однорідного многочлена другого степеня від двох змінних:
а) 1;
б) 2;
в) 3;
г) від 1 до 3.
18) Скільки членів може мати канонічна форма однорідного многочлена третього степеня від трьох змінних:
а) 3;
б) від 1 до 9;
в) від 1 до 10;
г) від 1 до 6.
19) Серед наступних одночленів вказати ті, які не можуть бути вищим членом многочлена:
а) 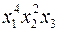 ;
;
б) 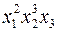 ;
;
в) 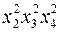 ;
;
г) 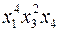 .
.
20) Многочлен  називається …, якщо внаслідок довільної перестановки змінних
називається …, якщо внаслідок довільної перестановки змінних 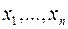 утворюється многочлен, рівний даному:
утворюється многочлен, рівний даному:
а) зведеним відносно змінних 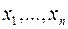 ;
;
б) симетричним відносно змінних 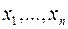 ;
;
в) звідним відносно змінних 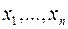 ;
;
г) однорідним відносно змінних 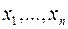 .
.
21) Якщо  є вищим членом симетричного многочлена, то:
є вищим членом симетричного многочлена, то:
а)  ;
;
б)  ;
;
в)  ;
;
г) 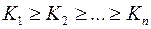 .
.
22) Що утворює множина всіх симетричних многочленів від 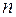 змінних над полем
змінних над полем  відносно дій додавання і множення:
відносно дій додавання і множення:
а) кільце з 1;
б) поле з 1;
в) групу з 1;
г) область цілісності з 1.
23) Як позначається такий елементарний симетричний многочлен  :
:
а) 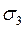 ;
;
б)  ;
;
в) 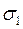 ;
;
г)  .
.
24) Чи вірно, що 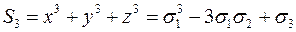 :
:
а) так;
б) ні;
в) якщо дописати 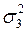 ;
;
г) якщо із запису вилучити 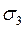 .
.
25) Чи можна всякий симетричний многочлен від 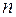 змінних подати у вигляді многочленів від основних симетричних функцій
змінних подати у вигляді многочленів від основних симетричних функцій 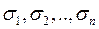 :
:
а) так;
б) ні;
в) залежить від вибору  ;
;
г) залежить від початкового многочлена.
26) Задача 1: знайти всі дійсні розв’язки системи рівнянь
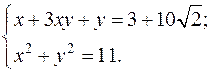
а) 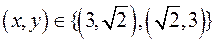 ;
;
б) 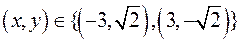 ;
;
в)  .
.
27) Задача 2: обчислити при яких раціональних значеннях  мають спільний корінь многочлени
мають спільний корінь многочлени  і
і 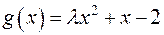 :
:
а) якщо  , то
, то 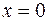 ;
;
б) якщо 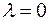 , то
, то 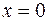 ;
;
в) якщо  , то
, то  .
.
28) Задача 3: знайти цілі значення  , при яких має кратні корені многочлен
, при яких має кратні корені многочлен  :
:
а)  ;
;
б) 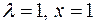 ;
;
в)  .
.
ТЕСТ 3
Дата добавления: 2015-08-21; просмотров: 217 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Подільність. Взаємнопрості многочлени. НСД та НСК многочленів. Раціональні дроби | | | Многочлени над різними полями |