Розділ III.Многочлени над полем комплексних чисел і над полем дійсних чисел

Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел

Питання для самоконтролю:

1) Яке поле називається алгебраїчно замкненим?

2) Скільки дійсних і комплексних коренів має многочлен з дійсними коефіцієнтами?

3) Сформулюйте основну теорему теорії многочленів.

4) Які многочлени називаються звідними у полі комплексних чисел?

5) Необхідна і достатня умова незвідності многочлена у
полі С: …

6) Скільки коренів має многочлен 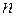-го степеня у полі комплексних чисел?

Задачі

1) Знайти многочлен найменшого степеня, в якого:
а) 1 – подвійний корінь, а 2, 3, – прості;
б) -1 – потрійний корінь, а 3 і 4 – прості.

2) Знайти многочлен найменшого степеня з дійсними коефіцієнтами, якщо – його потрійний корінь.

3) Знайти суму квадратів коренів многочлена

5) Сума двох коренів рівняння дорівнює 1. Визначити .

6) Використовуючи формули Вієта, побудувати многочлен за його коренями:

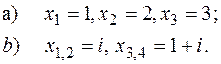
7) Знайти зведений многочлен, в якого корені задовольняють умову: , а , , 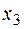є коренями многочлена .

8) Корені многочлена утворюють арифметичну прогресію. Знайти цей многочлен і його корені, якщо .

9) Чи утворюють корені рівняння арифметичну прогресію?

10) Визначте 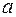так, щоб один з коренів многочлена був рівний подвоєному другому кореню.

Дата добавления: 2015-08-21