Дискримінант та результант двох многочленів, їх властивості і застосування до розв'язування задач

Питання для самоконтролю:

1) Що називається результантом?

2) Назвіть властивості результанту.

3) Щоб многочлени і мали спільний корінь необхідною і достатньою умовою є …

4) Як записується результант у формі Сільвестра?

5) Якщо , то …

6) Дискримінант двох многочленів - це …

7) Умова існування кратного кореня.

8) Який алгоритм виключення невідомих з системи рівнянь:

Задачі

1) Обчислити результант многочленів:
а) використовуючи означення;
б) використовуючи симетричні многочлени;
в) у формі Сільвестра.

2) При якому значенні мають спільні корені слідуючі многочлени:

3) Обчислити дискримінант многочленів:

4) Довести, що дискримінант многочлена 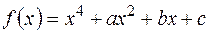дорівнює дискримінанту многочлена

5) При якому значенні многочлен має кратний корінь:

6) Розв’язати системи рівнянь:

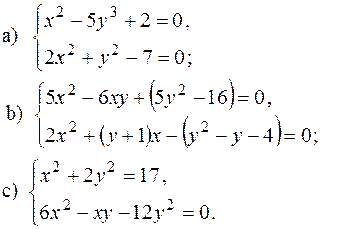
Дата добавления: 2015-08-21