Многочлени над полем дійсних чисел

Питання для самоконтролю:

1) Що можна сказати про спряжене комплексне число 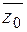, якщо комплексне число 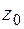є коренем многочлена з дійсними коефіцієнтами?

2) Який многочлен є звідним у полі дійсних чисел?

3) Як можна многочлен розкласти над полем дійсних чисел на незвідні множники?

Задачі

1) Розв’язати рівняння:

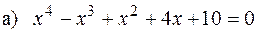, якщо ;
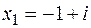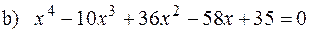, якщо ;

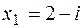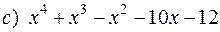, якщо .

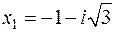2) Знайти нормований многочлен найменшого степеня з дійсними коефіцієнтами, що має:

а) простий корінь 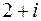і двократний корінь 1;

b) простий корінь 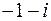і двократні корені 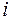та ;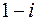

с) трикратний корінь .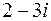

3) Знаючи, що число 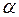є коренем многочлена , знайти інші його корені:

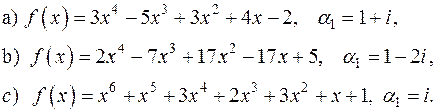
4) Розкласти многочлен на множники, незвідні над полем R:

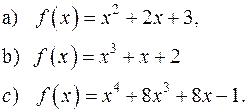
5) Яким умовам повинні задовольняти дійсні коефіцієнти многочлена:

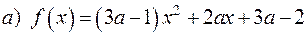, щоб він мав два різних дійсних корені;

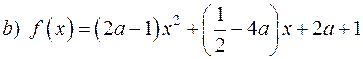, щоб він мав один дійсний корінь.

Дата добавления: 2015-08-21