Раціональні дроби. Елементарні дроби. Розклад дробу на елементарні дроби над полями Q,R і C

Питання для самоконтролю:

1) Який раціональний дріб називається правильним?

2) Елементарний дріб у полі 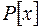- це …

3) Чи є елементарний дріб правильним?

4) Чи вірно, що 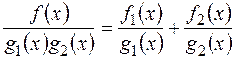, якщо 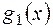і - взаємно прості многочлени? Відповідь пояснити.

5) Як можна представити правильний дріб ,

де - многочлен незвідний над полем ?

6) Чи єдиний розклад правильного дробу 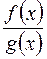на елементарні дроби у даному полі. Відповідь пояснити

Задачі

1) Довести тотожність:

2) Використовуючи інтерполяційну формулу Ньютона, побудувати многочлен найменшого степеня за такою таблицею:

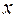
	-3	-2	-1

а)

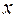
	-1

б)

3) Знайти многочлен найменшого степеня за такою таблицею:

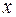
		і	-1	-і
	і		-і	-1

а)

Обчислити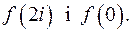

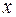
б) Обчислити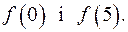

4) Знайти цілі числа такі, що

а) ;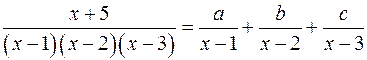

б) .

5) У полі 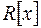знайти нескоротний дріб, який дорівнює
,
.

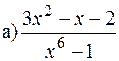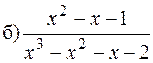6) Перевірити, чи є раціональні дроби 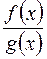елементарними над полем , якщо:

7) Розкласти дріб на елементарні дроби:

8) Розкласти дріб на елементарні дроби:

9) Розкласти дріб на елементарні дроби в полі комплексних чисел: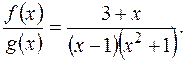

10) Розкласти дріб на елементарні дроби в полі раціональних чисел: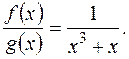

Дата добавления: 2015-08-21