
Читайте также:
|
а)  ;
;
б) 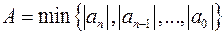 ;
;
в)  ;
;
г) 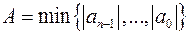 .
.
11) Щоб відокремити дійсні корені многочлена  необхідно знайти інтервали, у яких …
необхідно знайти інтервали, у яких …
а) не лежить жодного кореня;
б) лежить один корінь;
в) лежать два кореня;
г) лежать всі корені.
12) Якщо 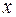 , зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь
, зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь 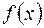 , то число змін знаків у ряді Штурма при цьому …
, то число змін знаків у ряді Штурма при цьому …
а) не зміниться;
б) зросте на 1;
в) зменшиться на 1.
13) Якщо 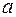 і
і  (
(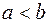 ) – довільні дійсні числа, які не є коренями
) – довільні дійсні числа, які не є коренями 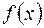 , то число
, то число 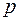 дійсних коренів многочлена
дійсних коренів многочлена 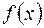 в інтервалі (
в інтервалі (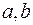 ) дорівнює
) дорівнює 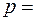 …, де
…, де 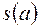 і
і  є число змін знаків у ряді Штурма відповідно у точках
є число змін знаків у ряді Штурма відповідно у точках 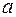 і
і  :
:
а) 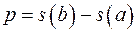 ;
;
б) 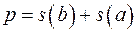 ;
;
в)  ;
;
г) 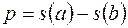 .
.
14) Яким є поле розкладу многочлена 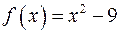 :
:
а) Z;
б) Q;
в) R;
г) C.
15) Яким є поле розкладу многочлена 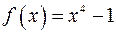 :
:
а) Z;
б) Q;
в) R;
г) C.
16) Яким є поле розкладу многочлена 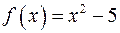 :
:
а) Z;
б) Q;
в) R;
г) C.
17) Коренем многочлена 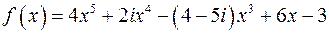
є …
а)  ;
;
б) 3;
в) 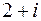 ;
;
г) 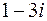 .
.
18) Чи є звідним над полем С многочлен  :
:
а) так;
б) ні;
в) при певному 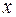 ;
;
г) можливо.
19) Яке максимальне число змін знаків може мати многочлен
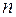 -го степеня:
-го степеня:
а) 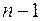 ;
;
б) 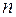 ;
;
в)  ;
;
г)  .
.
20) Щоб дріб 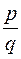 , де (
, де ( ) = 1 було коренем рівняння з цілими коефіцієнтами необхідно, щоб
) = 1 було коренем рівняння з цілими коефіцієнтами необхідно, щоб 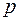 … многочлена
… многочлена 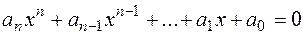 , а
, а  - …
- …
а) 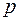 було дільником вільного члена, а
було дільником вільного члена, а  було б дільником старшого коефіцієнта;
було б дільником старшого коефіцієнта;
б) 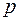 було дільником старшого коефіцієнта, а
було дільником старшого коефіцієнта, а  було б дільником вільного члена;
було б дільником вільного члена;
в) 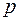 було дільником вільного члена, а
було дільником вільного члена, а  не було б дільником старшого коефіцієнта;
не було б дільником старшого коефіцієнта;
г) 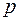 не було б дільником вільного члена, а
не було б дільником вільного члена, а  було б дільником старшого коефіцієнта.
було б дільником старшого коефіцієнта.
21) Щоб дріб 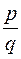 , де (
, де ( ) = 1 був раціональним коренем многочлена з цілими коефіцієнтами
) = 1 був раціональним коренем многочлена з цілими коефіцієнтами 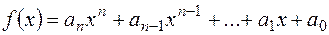 , необхідно, щоб при довільному цілому
, необхідно, щоб при довільному цілому 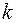 число
число 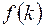
ділилося на …
а) 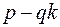 , де
, де 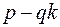
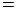 0;
0;
б)  , де
, де 
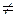 0;
0;
в) 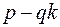 , де
, де 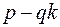
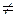 0;
0;
г)  , де
, де 
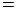 0.
0.
22) Якщо в многочлені з цілими коефіцієнтами 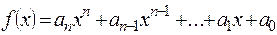 коефіцієнти
коефіцієнти 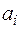 діляться на деяке просте число
діляться на деяке просте число 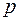 , причому
, причому  …, а старший коефіцієнт
…, а старший коефіцієнт 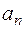 …, то многочлен
…, то многочлен 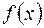 незвідний у полі раціональних чисел:
незвідний у полі раціональних чисел:
а)  не ділиться на
не ділиться на 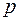 , і
, і 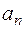 не ділиться на
не ділиться на 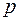 ;
;
б)  не ділиться на
не ділиться на 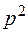 , і
, і 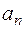 не ділиться на
не ділиться на 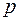 ;
;
в)  не ділиться на
не ділиться на 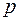 , і
, і 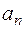 не ділиться на
не ділиться на 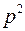 ;
;
г)  не ділиться на
не ділиться на 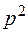 , і
, і 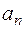 не ділиться на
не ділиться на 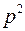 .
.
23) Многочлени  і
і 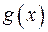 з кільця
з кільця 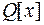 є взаємно простими. Чи можуть вони мати спільний комплексний корінь
є взаємно простими. Чи можуть вони мати спільний комплексний корінь 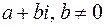 :
:
а) так;
б) ні;
в) при певному 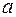 ;
;
г) при певному  .
.
24) Чи може незвідний у кільці 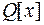 многочлен мати кратні комплексні корені
многочлен мати кратні комплексні корені 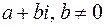 :
:
а) так;
б) ні;
в) при певному 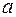 ;
;
г) при певному  .
.
25) Нехай є многочлен 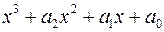 . Яка заміна приводить до многочлена виду
. Яка заміна приводить до многочлена виду 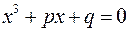 :
:
а) 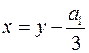 ;
;
б) 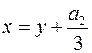 ;
;
в) 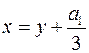 ;
;
г) 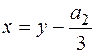 .
.
26) Якщо 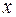 , зростаючи, проходить через корінь многочлена
, зростаючи, проходить через корінь многочлена 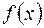 , то число змін знаків у ряді Штурма …
, то число змін знаків у ряді Штурма …
а) не зміниться;
б) зменшиться на 1;
в) збільшиться на 1.
27) Задача 1: знайти многочлен найменшого степеня, в якого число 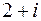 є трикратним коренем, -5 – двократним, а 3 є простим коренем:
є трикратним коренем, -5 – двократним, а 3 є простим коренем:
а) 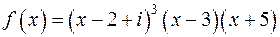 ;
;
б)  ;
;
в)  ;
;
г) 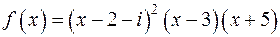 .
.
28) Задача 2: знайти суму квадратів коренів многочлена  :
:
а) 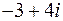 ;
;
б)  ;
;
в) 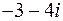 .
.
29) Задача 3: розв’язати рівняння 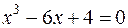 :
:
а) 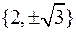 ;
;
б) 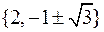 ;
;
в) 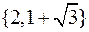 .
.
30) Задача 4: відокремити дійсні корені многочлена 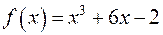 :
:
а) один комплексний корінь в інтервалі  ;
;
б) два дійсних кореня в інтервалі  ;
;
в) один дійсний корінь в інтервалі  .
.
31) Задача 5: знайти всі раціональні корені многочлена  :
:
а) 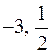 ;
;
б) 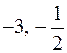 ;
;
в) раціональних коренів немає.
ТЕСТ 4
Дата добавления: 2015-08-21; просмотров: 157 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Многочлени над різними полями | | | Алгебраїчні розширення |