Читайте также:
|
Сделав предположение о существовании решения в виде произведения: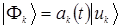 
, после подстановок, получим производную коэффициента 
: 
, откуда величина коэффициента может быть получена в виде гармонической функции: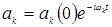 
, где, величина 
имеет смысл частоты гармонического колебания.
Применив условие нормировки 
к каждому из собственных векторов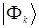 
, получим, с точностью до произвольного фазового множителя: 
Бра-вектор, соответствующий кет-вектору 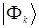, равен: 
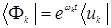, что следует из свойств скалярного произведения 
. Таким образом, при переходе от бра-векторов к кет-векторам и наоборот, постоянные заменяются комплексно сопряженными, а бра- и кет-векторы взаимозаменяются.
Специфической особенностью нормировки является то, что даже и в этом случае вектор не определен до конца. Вектор можно домножить на фазовый множитель, - число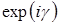 
с вещественным 
, и эта операция не меняет длины вектора.
Дата добавления: 2015-09-02; просмотров: 96 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Нормировка бра- и кет- векторов. | | | Запись уравнения Шредингера для кет-вектора и уравнение нормировки в обозначениях П.Дирака |