Калибратор фазы с линейным преобразованием управляющего кода в фазовый сдвиг

Широкое распространение получают калибраторы фазы, принцип действия которых заключается в суммировании двух синусоидальных напряжений, сдвинутых одно относительно другого на 90°. Диапазон регулирования фазового сдвига при этом составляет 0-90°, а его расширение до 360° осуществляется введением коммутатора опорных напряжений.

При регулировании фазового сдвига в пределах 0-90° выходное напряжение калибратора фазы формируется в соответствии с зависимостью

, (*)

где U_вх - амплитуды опорных напряжений;

k₁ и k₂ - весовые коэффициенты.

Амплитуда и фаза выходного напряжения связаны с весовыми коэффициентами k₁ и k₂ соотношениями

;

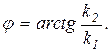
Калибраторы фазы, управляемые цифровым кодом, должны обеспечивать линейное преобразование управляющего кода в фазовый сдвиг выходного напряжения. Кроме того, в большинстве практических случаев необходимо обеспечивать постоянство амплитуды выходного напряжения во всем диапазоне регулирования фазового сдвига. Для выполнения этих требований весовые коэффициенты k₁ и k₂ должны быть связаны с управляющим кодом нелинейными зависимостями. В калибраторе фазы, структурная схема которого представлена на рис. 5, выходное напряжение является суммой двух синусоидальных напряжений U_s и U_c, сдвинутых одно относительно другого на 90°. Они формируются из входного напряжения U_вх цепью каскадно включенных цифроаналоговых преобразователей ЦАП1 - ЦАП7 и инвертирующими сумматорами А1 - А4.

Передаточная функция i -го ЦАП выражается линейной зависимостью

,

где b_i - масштаб преобразования i -го ЦАП;

N и N_max - текущее и максимальное значения управляющего кода.

Рисунок 5. Калибратор фазы с линейным преобразованием управляющего

кода в фазовый сдвиг

Применяемые в калибраторе фазы ЦАП имеют малое выходное сопротивление, что допускает их каскадное включение без нарушения нормального режима работы каждого отдельно взятого ЦАП. Поэтому передаточную функцию n каскадно включенных ЦАП с достаточной степенью точности можно записать в виде

На вход первого ЦАП, являющегося входом калибратора фазы, с внешнего генератора поступает синусоидальное напряжение 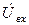. Из него цепью каскадно включенных ЦАП формируются напряжения, амплитуды U_n которых связаны с управляющим кодом соотношением

где

Напряжения с выходов ЦАП и входное напряжение используются для формирования двух синфазных напряжений и , причем напряжение формируется из входного напряжения и напряжений с выходов ЦАП с четными номерами, а выходные напряжения нечетных ЦАП используются для формирования напряжения 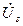. Полагая весовые коэффициенты суммируемых напряжений и , равными единице, и учитывая дополнительное инвертирование соответствующих напряжений сумматорами А1 и А3,зависимости амплитуды напряжений и от управляющего кода в соответствии с (4.5) можно представить в виде

U_s = - U_вх(a₁x- a₃x³+a₅x⁵- a₇x⁷) = U_вхk₂;

U_c = - U_вх(1- a₂x²+a₄x⁴- a₆x⁶) = U_вхk₁.

Таким образом, амплитуды напряжений и связаны с амплитудой синусоидального напряжения , поступающего на вход калибратора фазы, коэффициентами k₁ и k₂, которые в свою очередь имеют нелинейную зависимость от управляющего кода.

k₁ = 1- a₂x²+a₄x⁴- a₆x⁶;

k₂ = a₁x- a₃x³+a₅x⁵- a₇x⁷.

Чтобы получить фазовый сдвиг 90° между напряжениями и , одно из них, , подается на вход фазовращателя ФВ, в результате чего на входы сумматора А5 поступают напряжения U_c и jU_s. Выходное напряжение сумматора А5, являющееся выходным напряжением калибратора фазы, описывается соотношением (*).

Фаза определяется управляющим кодом, а амплитуда выходного напряжения зависит только от амплитуды входного напряжения U_вх (в рассмотренном случае U_вых = U_вх).

Разность между расчетными и заданными значениями фазы и амплитуды выходного напряжения будет тем меньше, чем точнее моделируются функциональные зависимости cosx и sinx.

Функции cosx и sinx могут быть представлены в виде суммы степенного ряда, причем тем точнее, чем больше членов степенного ряда при этом используется и чем меньше диапазон изменения аргумента x. Когда заданы число членов ряда и диапазон изменения переменной x, задача минимизации погрешности моделирования сводится к точному вычислению коэффициентов при суммирующихся членах ряда.

В табл. 2 приведены значения коэффициентов a_n, рассчитанные для трех случаев, когда высшая степень x и число ЦАП в схеме калибратора фазы соответственно равны семи, шести и пяти.

Методическая фазовая погрешность и нестабильность амплитуды выходного напряжения определяются соотношениями

.

Графики этих зависимостей приведены на рис. 6. (а, б) (где m - число ЦАП в схеме), а их максимальные значения указаны в табл.2.

Анализ полученных результатов показывает, что уже при использовании шести ЦАП можно построить калибратор фазы с высокими метрологическими характеристиками. Погрешность калибратора фазы в основном будет определяться погрешностью настройки ЦАП на заданный масштаб преобразования, паразитными фазовыми сдвигами в ЦАП и сумматорах на высоких частотах, а также, точностью поддержания фазового сдвига 90°.

Экспериментальная проверка макета калибратора фазы показала, что в диапазоне 30 Гц - 20 кГц основная погрешность не превышает 0,1° и достигает максимального значения на верхней частоте указанного диапазона. Испытания макета проводили с использованием калибратора фазы, прошедшего метрологическую аттестацию во ВНИИМ им. Д.И. Менделеева, г. Санкт-Петербург.

Таблица 2

Коэффициенты an	d Uвых, %	D j, °
a1 = 1,000 a2 = 0,4999 a3 = 0,1666 a4 = 0,0416 a5 = 0,0083 a6 = 0,0013 a7 = 0,0002	0,005	0,003
a1 = 1,000 a2 = 0,4999 a3 = 0,1661 a4 = 0,0416 a5 = 0,0076 a6 = 0,0013	0,016	0,005
a1 = 1,000 a2 = 0,4967 a3 = 0,16605 a4 = 0,03705 a5 = 0,00761	0,06	0,06

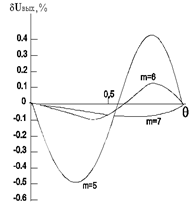Рис. 6. Зависимости погрешности фазового сдвига D j (а) и модуля dU_вых напряжения выхода (б)

Контрольные вопросы

1. Что представляет собой цифроаналоговый преобразователь (ЦАП)?

2. Перечислить параметры цифроаналоговых преобразователей.

3. Резисторная матрица R – 2R и ее применение в цифроаналоговых преобразователях.

4. Что такое умножающие ЦАП?

5. Нарисовать схему включения умножающего ЦАП для четырехквадрантного умножения.

6. Привести схему функционального ЦАП, использующего линейную аппроксимацию.

7. Чем определяется методическая погрешность функционального ЦАП?

8. Привести формулы для расчета элементов функционального ЦАП, если входное сопротивление линейного ЦАП равно R_О. Расчетные формулы привести для воспроизведения функции sinφ в диапазоне [0, 90 град.].

9. Нарисовать схему функционального ЦАП с каскадным соединением линейных ЦАП.

10. Привести принципиальную схему и параметры ЦАП К572ПА1.

СПИСОК ЛИТЕРАТУРЫ

1. Федорков Б.Г., Телец В.А., Дегтяренко В.П. Микроэлектронные цифро-аналоговые и аналого-цифровые преобразователи.- М.: Радио и связь, 1984.- 320 с.

2. Гутников В.С. Интегральная электроника в измерительных устройствах. – 2-е изд. – Л.: Энергоатомиздат, 1988. – 304 с.

3. Арутюнов В.О. Электрические измерительные приборы и измерения. Госэнергоиздат, 1958. – 632 с.

4. Сапельников В.М., Хакимов Р.А., Газизов А.А., Шабанов М.А. Функциональные цифроаналоговые преобразователи: принципы построения // Датчики и системы, 2007. - № 7, - С. 46 – 57.

5. Мелик-Шахназаров А.М. Потенциометрический фазовращатель. Радиотехника, 1957. Т. 12, - №5,. - С. 78-79.

6. Сапельников В. М. ЦАП в калибраторах фазы / Изд-е Башкирск. ун-та. - Уфа, 1997. - 152 с.

7. Сапельников В.М., Кравченко С.А., Чмых М.К. Проблемы воспроизведения смещаемых во времени электрических сигналов и их метрологическое обеспечение / Изд-е Башкирск. гос. ун-та. – Уфа, 2000. – 196 с.

8. Электроника: Справочная книга / Под ред. Ю.А. Быстрова. - СПб.: Энергоатомиздат, 1996. - 544 с.

Дата добавления: 2015-08-21