Два вектора плоскости линейно зависимы тогда и только тогда они коллинеарны.Два вектора плоскости линейно независимы в том и только том случае, если они не коллинеарны.

9. Скалярное произведение векторов. Условие перпендикул. двух векторов. Механический смысл скалярного произведения векторов.

Скалярным произведением двух ненулевых векторов называется число, равное произведению длин векторов на косинус угла между ними:

Скалярное произведение обозначают символом , или , или .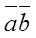

Механический смысл скалярного произведения. Скалярное произведение двух векторов численно равно работе некоторой силы при перемещении тела под действием этой силы.

Условие перпендикулярности двух векторов. Два ненулевых вектора и перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

10. Ориентация тройки векторов в пространстве. Векторное произведение векторов. Физический смысл векторного произведения векторов. Условие коллинеарности векторов.

Ориентация тройки векторов в пространстве. Тройку векторов называют упорядоченной, если указано, какой из векторов считается первым, какой вторым и какой третьим.

Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу кратчайший поворот от первого ко второму вектору наблюдается с конца третьего вектора против часовой стрелки. В противном случае указанная тройка векторов называется левой.

Векторным произведением векторов и называется вектор , длина которого численно равна площади параллелограмма, построенного на векторах и , приведенных к общему началу, который перпендикулярен перемножаемым векторам и направлен так, что векторы образуют правую тройку векторов.

Если векторы и коллинеарны, то их векторное произведение равно нулевому вектору.

Векторное произведение двух векторов и 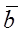обозначают символом , или , или .

Физический смысл векторного произведения. Таким образом, момент силы относительно некоторой точки , есть векторное произведение радиус–вектора точки приложения силы на вектор силы :

Два ненулевых вектора и коллинеарны тогда и только тогда, когда их координаты пропорциональны:

11. Смешанное произведение векторов. Условие компланарн. трех векторов.

Пусть даны три вектора 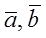и . Умножим вектор векторно на , а полученный вектор умножим скалярно на и тем самым определим число . Оно называется векторно-скалярным или смешанным произведением трех векторов 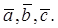обозначают также , или , или .

Смешанное произведение выражается:

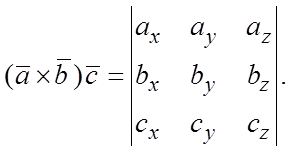
Необходимым и достаточным условием компланарности векторов является равенство нулю их смешанного произведения: .

12. Различные виды уравнений прямой на плоскости. Взаимное расположение двух прямых на плоскости. Угол между прямыми. Расстояние от точки до прямой.

Уравнение прямой с угловым коэффициентом:

Уравнение прямой, проходящей через данную точку,
с данным угловым коэффициентом:

Уравнение прямой, проходящей через две данные точки:

Общее уравнение прямой: Уравнение прямой в «отрезках»:

Ax + By + C = 0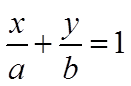

Взаимное расположение двух прямых на плоскости: Две прямые на плоскости либо пересекаются в одной точке, либо совпадают, либо параллельны.

Один из углов между прямыми определяется условием:

а второй угол равен .

Расстояние от точки до прямой, заданной общим уравнением 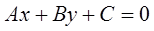, определяется равенством:

13. Эллипс. Его характеристики.

Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек F₁ и F₂, называемых фокусами, есть величина постоянная, равная 2a.

Каноническое уравнение эллипса: (1)

Параметр b² определяется равенством b² = a² – c². Эллипс симметричен относительно обеих осей координат. Эллипс пересекает ось Ox в двух точках: A(a;0) и A₁(-a;0),пересекает ось Oy в двух точках: B(0; b) и B₁(0; -b). Эти четыре точки называют вершинами эллипса. Отрезок A₁A называется большой осью эллипса, а отрезок B₁B – его малой осью. Здесь a > b.

Уравнение (1) можно рассматривать и в случае a < b. Тогда оно определяет эллипс с большой полуосью OB = b, фокусы такого эллипса лежат на оси Oy.

В случае, когда a=b, уравнение (1) имеет вид x² + y² = a² и определяет окружность радиуса а, с центром в начале координат. В этом случае c = 0.

Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси, т.е. .

Поскольку с < a, то для любого эллипса , причем случай соответствует окружности.

Геометрически характеризует степень сжатия эллипса: чем больше , тем больше вытянут эллипс.

Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии от него, называются директрисами эллипса.

Если эллипс задан каноническим уравнением (1), то уравнения директрис имеют вид

и .

14. Гипербола. Ее характеристики.

Гиперболой называется множество точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек F₁ и F₂, называемых фокусами, есть величина постоянная, равная 2a< | F₁ F₂ |.

Канон. уравнение гиперболы: 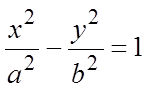, где .(1)

Гипербола пересекает ось Ox в двух точках: A(a;0) и A₁(-a;0), называемых вершинами гиперболы. Отрезок A₁A = 2a называется действительной осью гиперболы, а отрезок B₁B=2b – мнимой.

Прямые называются асимптотами гиперболы, к которым приближаются ветви гиперболы при увеличении х по абсолютной величине. Эксцентриситетом гиперболы называют отношение . Чем меньше , т.е. чем ближе к единице, тем больше вытянут основной прямоугольник по оси Ох.

Если у гиперболы a=b, то она называется равносторонней и ее уравнение принимает вид x² – y² = a². Асимптотами этой гиперболы являются взаимно перпендикулярные прямые .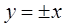

Уравнение (2)

определяет гиперболу с действительной осью Oy.

Гиперболы, определяемые уравнениями (1) и (2) в одной и той же системе координат с одинаковыми значениями и , называются сопряженными.

Две прямые, заданные уравнениями и , называют директрисами гиперболы. Правая директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной гиперболы.

15. Парабола. Ее характеристики.

Параболой называется множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и от данной прямой L, называемой директрисой.

Параметр параболы – расстояние от фокуса до директрисы.

Каноническое уравнение параболы:

Уравнение имеет смысл только для неотрицательных значений х, т.е. все точки параболы лежат в I и IV квадрантах. Парабола симметрична относительно оси Ох.

Точка О называется вершиной параболы, ось симметрии (ось Ох)– осью параболы. Параметр р характеризует «ширину» области, ограниченной параболой.

Парабола, определяемая уравнением , расположена слева от оси ординат. Ее вершина совпадает с началом координат О, осью симметрии является ось Ох.

Уравнение , является уравнением параболы с вершиной в точке О и осью симметрии Оу. Такая парабола лежит выше оси абсцисс. Уравнение , определяет параболу, которая лежит ниже оси Ох, с вершиной в точке О и осью симметрии Оу.

16. Уравнение кривых второго порядка в полярной системе координат.

Утверждение 1. Отношение расстояния r от произвольной точки эллипса (гиперболы) до фокуса к расстоянию d от этой точки до соответствующей директрисы есть постоянная величина, равная эксцентриситету эллипса (гиперболы), т.е. .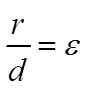

Заметим, что таким же свойством обладает и парабола, если считать .

Дата добавления: 2015-08-21