Уравнения эллипса, гиперболы, параболы в полярных координатах.

Обозначим через F фокус кривой, через – директрису. Введем полярную систему координат таким образом, что ее полюсом является точка F, а ось перпендикулярна директрисе (рис. 3).

Утверждение 2. Уравнение

(1)

во введенной системе координат определяет эллипс, если ; гиперболу, если и параболу, если .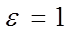

Уравнение (1) называется полярным уравнением эллипса, параболы, гиперболы. В случае гиперболы это уравнение определяет одну из двух ее ветвей. Отметим, что для параболы параметр р в уравнении (1) совпадает с ее параметром р из §10, а для эллипса и гиперболы

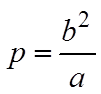
17. Различные способы задания плоскости в пространстве. Взаимное расположение плоскостей. Угол между плоскостями. Расстояние от точки до плоскости.

Общее уравнение плоскости: Ax +By + Cz + D = 0

Уравнение плоскости, проходящей через три данные точки

Уравнение плоскости в отрезках:

Условие параллельности плоскостей (1) совпадет с условием коллинеарности векторов и и имеет вид

.

Отсюда вытекает также условие совпадения плоскостей (1):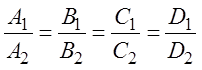

Условие перпендикулярности плоскостей (1) есть вместе с тем и условие перпендикулярности нормальных векторов и :

.

Углом между плоскостями называется любой из двух смежных двугранных углов, образованных этими плоскостями. Сумма этих смежных двугранных углов равна . Один из этих углов определяется как угол между нормальными векторам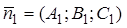и и к этим плоскостям:

.

Расстояние d от точки до плоскости находится по формуле

.

18. Прямая в пространстве. Способы ее задания. Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми.

Прямая может быть задана пересечением двух плоскостей:

Параметрические уравнения:

Каноническое уравнение:

Углом между двумя прямыми считают один из двух смежных углов, которые образуют прямые, проведенные параллельно данным через какую-нибудь точку пространства.

Условие параллельности прямых совпадает с условием коллинеарности векторов: .

Условие перпендикулярности прямых равносильно условию перпендикул. их направляющих векторов: l₁l₂+m₁m₂+n₁n₂=0

Условие расположения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых), имеет вид:

Если величины 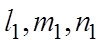не пропорциональны величинам , то условие является необходимым и достаточным условием пересечения двух прямых в пространстве.

19. Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью.

Углом между прямой L и плоскостью S считают острый угол α между этой прямой и ее проекцией на плоскость S (рис.1).

Этот угол определяется равенством:

Условие параллельности прямой и плоскости:

Al + Bm +Cn = 0

Прямая перпендикулярна плоскости в том и только том случае, когда направляющий вектор этой прямой коллинеарен нормальному вектору плоскости, что равносильно следующему равенству:

Прямая принадлежит плоскости тогда и только тогда, когда одновременно будут выполняться два равенства:

где первое из равенств означает, что точка , через которую проходит прямая, принадлежит плоскости, а второе равенство из выражает условие параллельности прямой и плоскости.

20. Конические поверхности.

Конической называется поверхность, описываемая прямой, движущейся вдоль некоторой линии и проходящей через некоторую точку. Уравнение конуса второго порядка с вершиной в начале координат, осью которого служит ось Oz, записывается в виде:

Геометрически коническую поверхность можно изобразить:

Аналогично, уравнения , являются уравнениями конусов второго порядка с вершиной в начале координат, осями которых служат соответственно оси Оу, Ох.

21. Цилиндрические поверхности.

Поверхность, описываемая прямой, движущейся вдоль некоторой линии и остающейся параллельной некоторому заданному направлению, называется цилиндрической.

Уравнение вида F(x, y) = 0 в декартовой системе координат
в пространстве определяет цилиндрическую поверхность, у которой образующие параллельны оси Oz. Аналогично, уравнение F(x, z) = 0 определяет цилиндрическую поверхность с образующими параллельными оси Oy, а F(y, z) = 0 – цилиндрическую поверхность с образующими параллельными оси Ох.

Канонические уравнения цилиндров второго порядка:

эллиптический цилиндр

гиперболический цилиндр

параболический цилиндр

Образующие всех трех цилиндров, определяемых уравнениями, параллельны оси Oz, а направляющей служит соответствующая кривая второго порядка (эллипс, гипербола, парабола), лежащая в плоскости Oxy.

Отметим, что кривую в пространстве можно задать либо параметрически, либо в виде линии пересечения двух поверхностей. Например, уравнения направляющей эллиптического цилиндра, т.е. уравнения эллипса в плоскости Oxy, имеют вид

22. Эллипсоид.

Эллипсоидом называется поверхность, определяемая в декартовой системе координат Oxyz каноническим уравнением

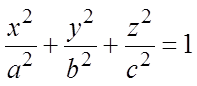
где величины а, b, c называют полуосями эллипсоида. Точки пересечения осей координат с эллипсоидом называют вершинами эллипсоида.

Плоскость Oхz пересекает эллипсоид по эллипсу, который определяется системой

плоскость Oyz – по эллипсу, определяемому уравнениями

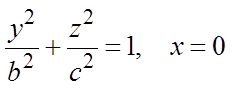
Если две полуоси эллипсоида равны, например a = b, получаем:

Если пересечь эллипсоид плоскостью z = h, то получим окружность

с центром на оси Oz. Поэтому такой эллипсоид можно получить вращением расположенного в плоскости Oхz эллипса вокруг оси Oz. Эллипсоид называют эллипсоидом вращения.

Отметим также, что в случае a = b = c эллипсоид является сферой.

23. Гиперболоиды.

Однополостным гиперболоидом называется поверхность, которая в декартовой системе координат Oxyz определяется каноническим уравнением:

Однополостный гиперболоид изображается в виде бесконечной трубки, бесконечно расширяющейся в обе стороны по мере удаления от плоскости Оху.

Двуполостным гиперболоидом называют поверхность, определяемую в декартовой системе координат Oxyz каноническим уравнением

Двуполостный гиперболоид изображается в виде поверхности, состоящей из двух отдельных «полостей», каждая из которых имеет вид бесконечной выпуклой чаши.

Величины a, b, c называют полуосями двуполостного гиперболоида. Если полуоси a и b гиперболоида (однополостного или двуполостного) равны, то он называется гиперболоидом вращения и получается вращением вокруг оси Oz гиперболы в случае однополостного гиперболоида и гиперболы в случае двуполостного гиперболоида.

24. Параболоиды.

Эллиптическим параболоидом называется поверхность, определяемая в декартовой системе координат Oxyz каноническим уравнением

Гиперболическим параболоидом называется поверхность, определяемая каноническим уравнением

Из уравнений (1) и (2) вытекает, что плоскости Oxz и Oyz являются плоскостями симметрии параболоидов.

Ось Oz называется осью параболоида, а точка ее пересечения с поверхностью параболоида – вершиной.

При эллиптический параболоид, заданный уравнением

,

называется параболоидом вращения. Он получается при вращении параболы вокруг оси Oz.

25. Линейное векторное пространство. Подпространство. Линейная зависимость и независимость векторов линейного пространства. Базис и размерность линейного пространства. Координаты векторов. Преобразование координат вектора при замене базиса.

Векторное (линейное) пространство — это математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр.

Пусть задано множество W, в котором определены те же операции, что и в линейном пространстве V. Множество назовем подпространством линейного пространства V, если выполнены следующие условия: 1) если , то 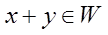; 2) если , то . Система векторов 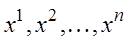называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, т.е:

Если равенство выполняется только в случае 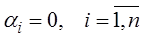, то система векторов называется линейно независимой.

Базис и размерность. Линейное пространство называется конечномерным, если существует такое натуральное число n, что в этом пространстве найдетсясистемаиз n линейно независимых векторов, а любая система из (n+1) вектора является линейно зависимой. Число n в этом случае называется размерностью пространства.

Базисом n -мерного линейного пространства V называется любая упорядоченная система n линейно независимых векторов этого пространства.

называется разложением вектора x по базису , а коэффициенты – координатами вектора x в базисе . Если вектор x в некотором базисе имеет координаты , то записывают .

26. Евклидово пространство. Неравенство Буняковского-Коши. Ортогональный и ортонормированный базисы. Разложение вектора по ортогональному базису.

Евклидовым пространством называется линейное действительное пространство, в котором задана операция скалярного умножения векторов, удовлетворяющая аксиомам:

1) ; 2) ; 3) ;

4) при для .

Неравенство Коши-Буняковского:

Векторы x и y евклидова пространства V называются ортогональными , если выполняется условие .

Вектор x евклидова пространства V назовем нормированным или единичным, если .

Система векторов называется ортонормированной, если она является ортогональной и нормированной.

Базис n -мерного евклидова пространства V называется ортонормированным, если базисные векторы образуют ортонормированную систему. В n -мерном евклидовом пространстве V существует ортонормированный базис.

27. Линейные операторы. Матрица линейного оператора. Действия над линейными операторами. Зависимость между матрицами линейного оператора в различных базисах.

Оператор линейного пространства V называется линейным оператором, если для любых векторов x и y из V и каждого действительного числа λ выполняются условия:

Матрицу

i- тый столбец которой состоит из координат вектора yⁱ, , называют матрицей линейного оператора А в базисе 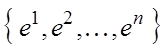и обозначают А (для матрицы оператора сохраним то же обозначение, что и для линейного оператора).

Суммой операторов А и В называют линейный оператор , который каждому вектору 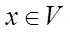ставит в соответствие вектор

Произведением линейного оператора на число называют оператор , который каждому вектору ставит в соответствие вектор . Матрица оператора в заданном базисе равна произведению матрицы оператора А на число .

Результат последовательного использования двух линейных операторов , называют их произведением и обозначают (оператор, который выполняется первым, записывают с правой стороны), т.е. Если в пространстве V задать базис и обозначить через А матрицу оператора А, а через В матрицу оператора В в этом базисе, то матрица оператора в том же базисе равна произведению матриц В и А.

28. Собственные векторы и собственные значения матриц и их свойства. Характеристическое уравнение и многочлен матрицы. Приведение матрицы к диагональному виду.

Пусть A – линейный оператор в n-мерном линейном пространстве V, определяемый матрицей A порядка n.

Собственным вектором данного линейного оператора называется такой ненулевой вектор 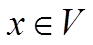, который удовлетворяет условию

причем λ – действительное число, называемое собственным числом или собственным значением оператора A, а x называется собственным вектором.

1) Собственный вектор линейного оператора имеет единственное собственное значение λ.

2) Если x – собственный вектор линейного оператора с собственным значением λ и 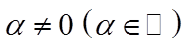, то – также собственный вектор оператора A с собственным значением λ.

3) Если x и y – линейно независимые собственные векторы линейного оператора A с одним и тем же собственным значением λ, то x+y – также собственный вектор этого оператора с собственным значением λ.

4) Если x и y – собственные векторы линейного оператора с различными собственными числами λ₁ и λ₂ (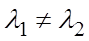), то x и y – линейно независимы.

Характеристическое уравнение:

Характеристический многочлен:

29. Квадратичные формы и их матрицы. Приведение квадратичной формы к каноническому виду. Знакоопределённые квадратичные формы. Условия знакоопределённости квадратичных форм.

Квадратичной формой называется выражение:

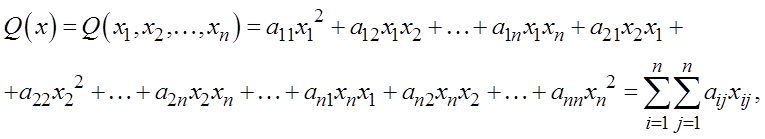
где вещественные числа a_ij называются коэффициентами квадратичной формы.

Из коэффициентов составим симметрическую матрицу,

которую назовем матрицей квадратичной формы.

Квадратичная форма называется канонической, если она не содержит произведений различных переменных, т.е. имеет вид:

Любая квадратичная форма невырожденным преобразованием может быть приведена к каноническому виду.

Квадратичная форма называется положительно определенной, если она приводится к нормальному виду, состоящему из n положительных квадратов, т.е.

Квадратичная форма является положительно определенной тогда и только тогда, когда она принимает положительные значения при любой ненулевой системе значений переменных.

Квадратичная форма является положительно определенной тогда и только тогда, когда все ее главные миноры положительны.

Квадратичная форма называется отрицательно определенной, если она является невырожденной и приводится к нормальному виду, содержащему только отрицательные квадраты всех переменных.

Положительно определенные и отрицательно определенные квадратичные формы называют знакоопределенными квадратичными формами.

Вырожденные квадратичные формы, нормальный вид которых состоит из квадратов переменных одного знака, называют полуопределенными (соответственно неотрицательными, неположительными).

Неопределенными называют квадратичные формы, нормальный вид которых содержит как положительные так и отрицательные квадраты переменных.

30. Множество действительных чисел. Модуль действительного числа. Ограниченные и неограниченные числовые множества. Наибольший и наименьший элементы числового множества. Верхняя и нижняя грани числового множества.

Прямую, на которой указаны начало отсчета, масштаб и направление отсчета, называют числовой осью. На числовой оси удобно изображать числовые множества.

Числовое множество называется ограниченным сверху, если существует такое действительное число 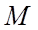, что для каждого элемента рассматриваемого множества выполняется неравенство . При этом число называется верхней гранью рассматриваемого множества.

рисунок

Числовое множество называется ограниченным снизу, если существует такое действительное число m, что для каждого элемента x рассматриваемого множества выполняется неравенство . При этом число называется нижней гранью рассматриваемого множества.

Ограниченное сверху (снизу) множество имеет бесконечно много верхних (нижних) границ.

Числовое множество называется ограниченным, если оно ограничено снизу и сверху.

Наименьшая из верхних граней множества называется точной верхней гранью этого множества. Наибольшая из нижних граней множества называется точной нижней гранью этого множества. Точная верхняя грань множества A обозначается (от латинского supremum), точная нижняя грань множества A обозначается (от латинского infimum).

Равенство равносильно выполнению дух требований 1) , 2) .

Равенство равносильно выполнению дух требований 1) , 2) .

Если непустое множество действительных чисел ограничено сверху (снизу), то оно имеет точную верхнюю (точную нижнюю) грань.

31. Понятие предела числовой последовательности. Бесконечно малые числовые последовательности и их свойства. Свойства сходящихся последов-тей. Монотонные последовательности, теорема Вейерштрасса.

Число a называется пределом последовательности { x_n }, если <-N такое, что и обозначается .

Последовательность { x_n } называется бесконечно малой, если ее предел равен нулю. Бесконечно малыми, например, являются последовательности .

Основные свойства бесконечно малых последовательностей:

1. Сумма конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

2. Бесконечно малая последовательность ограничена.

3. Произведение бесконечно малой последовательности и ограниченной последовательности есть бесконечно малая последовательность. 4. Произведение нескольких бесконечно малых последовательностей есть бесконечно малая последовательность. Свойства сходящихся послед-тей:

1. Для того, чтобы число а было пределом последовательности { x_n }, необходимо и достаточно, чтобы x_n имело вид , где – бесконечно малая последовательность.

2. Сходящаяся последовательность имеет только один предел.

3. Сходящаяся последовательность ограничена.

4. Пусть и , где и 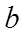- конечные числа.

Тогда: а) ; б) ;

в) (при условии, что ).

Возрастающая и убывающая послед-ти называются монотонными послед-тями. Вейерштрасса: Всякая монотонная ограниченная последовательность имеет предел.

32. Понятие функции. Предел функции в точке и на бесконечности. Односторонние пределы. Свойства функций, имеющих предел.

Возьмем: y = 2x

Переменная х называется независимой переменной или аргументом функции, переменная у – зависимой переменной или функцией. Множество Х называют областью определения или областью существования функции f. Множество всех значений у, ,называется областью значений функции.

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом и правосторонним пределом.

1. Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра.

2. Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.

33. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых функций. Эквивалентные функции и их применение к вычислению пределов.

Функция называется бесконечно малой при 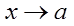, если .

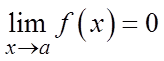Функция 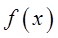называется бесконечно большой при , если .

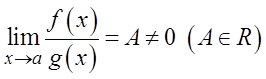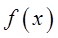1. Если , то и называются бесконечно малыми одного порядка. 2. Если , то называется бесконечно малой более высокого порядка, чем .

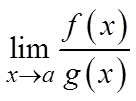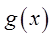3. Если , то называется бесконечно малой более низкого порядка, чем . 4. Если не существует, то и называются несравнимыми бесконечно малыми функциями.

Для раскрытия неопределенностей вида бывает полезным применять замену бесконечно малой функции на эквивалентную

1. при ; 2. 3.

4. 5. 6.

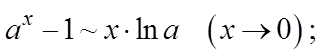7. 8.

9.

10. в частности

34. Непрерывность функции в точке и на отрезке. Свойства функций, непрерывных в точке.

Пусть функция определена в некоторой окрестности точки . Функция называется непрерывной в точке а, если:

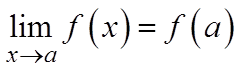
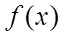Если , то функция называется непрерывной в точке а справа; если , то – непрерывной в точке а слева.

Функция называется непрерывной на интервале , если она непрерывна в каждой точке . См. 37 для отрезка.

Дата добавления: 2015-08-21