Метод Гаусса.

Распространенным точным методом решения систем линейных алгебраических уравнений является метод Гаусса, который применяется для решения произвольных систем линейных алгебраических уравнений. Суть метода состоит в том, что посредством элементарных преобразований система линейных алгебраических уравнений приводится к треугольной или трапециевидной форме (прямой ход метода Гаусса), при помощи которой непосредственно получаются все решения системы (обратный ход метода Гаусса).

На практике прямой ход метода Гаусса как правило применяется не к системе уравнений, а к ее расширенной матрице .

Пример 1. Решить систему

Решение. Последовательно получаем следующие матрицы:

По последней матрице записываем систему уравнений, равносильную данной:

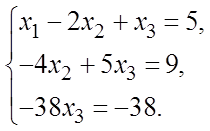
Начиная снизу вверх, последовательно находим: , Итак, (2; –1; 1) – единственное решение данной системы.

7. Однородные системы линейных алгебраических уравнений. Фундаментальная система решений.

Однородная система уравнений есть частный случай системы

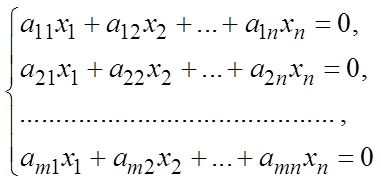(1)

есть частный случай системы линейных алгебраических уравнений. Система (1) всегда имеет нулевое решение , и поэтому она совместна. Нулевое решение является единственным тогда, когда ранг матрицы системы равен количеству неизвестных n.

Утверждение 1. Любая линейная комбинация решений однородной системы линейных уравнений есть также решение этой системы.

Решения , , …, однородной системы называют линейно зависимыми, если столбцы матрицы

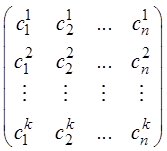(2)

линейно зависимые. В противном случае решения называют линейно независимыми.

Утверждение 2. Пусть ранг r матрицы А однородной системы (1) меньше количества неизвестных n. Тогда существует (n - r) линейно независимых решений 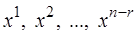этой системы, причем каждое ее решение есть линейная комбинация решений

Совокупность максимального количества линейно независимых решений однородной системы (1) называют фундаментальной системой решений.

8. Декартова система координат. Понятие вектора. Линейные операции над векторами. Координаты вектора. Линейная зависимость и независимость векторов. Понятие базиса.

Декартова система координат в пространстве.Система координат Охуz определяется заданием масштабной единицы измерения длин и трех пересекающихся в одной точке взаимно перпендикулярных осей: Ох, Оу, Оz. Точка О – начало координат, Ох – ось абсцисс, Оу – ось ординат, Оz – ось аппликат. Декартова система координат в пространстве устанавливает взаимно однозначное соответствие между множеством всех точек пространства и множеством упорядоченных троек чисел. Плоскости Оху, Оуz, Охz назовем координатными плоскостями. Они делят все пространство на восемь частей, называемых октантами.

Свободным вектором называется направленный отрезок (определены начало и конец) при произвольности его положения на плоскости или в пространстве. Направление вектора на рисунке указывают стрелкой. Вектор нулевой длины называется нулевым и обозначается .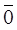

Связанным вектором с началом в точке А и концом в точке В называют направленный отрезок, в котором точка А является началом, а точка В – концом. Начало вектора называют еще точкой его приложения.

Суммой называется вектор, который имеет началом начало вектора и концом – конец вектора при условии, что начало вектора совпадает с концом вектора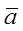

Разностью векторов и называется вектор , который в сумме с вектором 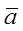дает вектор .

Произведением называют вектор, который коллинеарен вектору 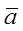, имеет длину, равную , и направление такое же, как и вектор 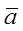, если , и противоположное

Пусть в пространстве задана декартова система координат и произвольный вектор . Если известны координаты начала и конца вектора: и , то координаты вектора определяются формулами: .

Рассмотрим декартову систему координат Охуz. Пусть – единичные векторы соответствующих осей координат Ох, Оу, Оz, т.е. и каждый из них одинаково направлен с соответствующей осью координат (рис. 1). Тройка векторов называется базисом.

Дата добавления: 2015-08-21