Свойства функций, непрерывных в точке

1. Пусть функции и непрерывны в точке . Тогда функции также непрерывны в этой точке (последняя при условии, что ).

2. Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция непрерывна в точке .

35. Точки разрыва функции и их классификация. Непрерывность элементарных функций.

Точка а называется точкой разрыва функции , если функция не является непрерывной в этой точке.

Точка а называется точкой разрыва первого рода функции 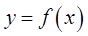, если в этой точке существуют конечные пределы функции слева и справа, т.е. и 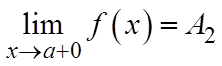. При этом:

а) если 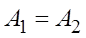, то точка а называется точкой устранимого разрыва; б) если , то точка а называется точкой конечного разрыва. Величину 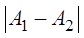называют скачком функции в точке разрыва .

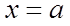Точка а называется точкой разрыва второго рода функции , если, по крайней мере, один из односторонних пределов (слева или справа) не существует.

Функция называется непрерывной на интервале , если она непрерывна в каждой точке . Если же, кроме того, функция непрерывна в точке а справа, а в точке – слева, то функция называется непрерывной на отрезке .

Функция называется кусочно-непрерывной на отрезке 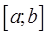, если она непрерывна во всех внутренних точках , за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и имеет соответствующие односторонние пределы.

36. Замечательные пределы.

Предел функции при . Имеет место соотношение

называемое первым замечательным пределом.

Эти равенства называют вторым замечательным пределом.

38. Обратная функция и её непрерывность.

Если функция непрерывна и монотонна на отрезке , то на множестве ее значений 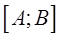существует монотонная, непрерывная обратная функция.

Функции , обратные функциям , в силу названного свойства непрерывны при всех значениях , при которых эти функции определены.

39. Производная функции, её геометрический и физический смысл.

Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю.

37. Функции, непрерывные на отрезке, и их свойства. Теоремы Больцано-Коши о промежуточном значении.

Функция называется непрерывной на интервале , если она непрерывна в каждой точке . Если же, кроме того, функция непрерывна в точке а справа, а в точке b – слева, то функция называется непрерывной на отрезке .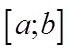

Функция называется кусочно-непрерывной на отрезке, если она непрерывна во всех внутренних точках, за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и b имеет соответствующие односторонние пределы.

Первая теорема Больцано-Коши. Пусть функция непрерывна на отрезке 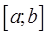и на концах отрезка имеет значения разных знаков. Тогда существует точка , в которой .

Вторая теорема Больцано-Коши. Пусть функция непрерывна на отрезке , причем . Тогда, если С – любое число, лежащее строго между и , то существует точка , такая, что .

40. Правила дифференцирования, производная сложной и обратной функции. Производные элементарных функций.

Правила дифференцирования. Если функции и имеют производныев точке x, то сумма, разность, произведение и частное этих функций также имеют производную в этой точке (частное при условии, что ) и справедливы следующие формулы:

, , .

Производная сложной функции. Если функция имеет в точке производную, а функция 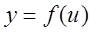имеет в соответствующей точке производную , то сложная функция имеет производную в точке 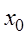и справедлива следующая формула:

Производная обратной функции. Если функция строго монотонна и непрерывна в некоторой окрестности точки , имеет производную в точке и , то обратная функция имеет производную в соответствующей точке , , причем .

41. Дифференцирование функций, заданных параметрически и неявно. Производные и дифференциалы высших порядков. Формула Лейбница.

Производная неявной функции. Пусть функция задана неявно: .

Для нахождения производной 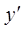будем дифференцировать обе части равенства, считая, что x – независимая переменная, а y есть функция переменной x. Из полученного уравн. найдем .

Будем говорить, что переменная y как функция аргумента x задана параметрически, если обе переменные x и y заданы как функции некоторой третьей переменной t, называемой параметром.

Производные высших порядков Производной второго порядка функции называется производная от производной первого порядка , если она существует, и обозначается .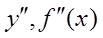

Производную от второй производной называют производной третьего порядка и обозначают .

Аналогично производная n-го порядка является производной от производной -го порядка и обозначается .

Формула Лейбница:

42. Дифференциал функции и его геометрический смысл. Применение дифференциала в приближённых вычислениях. Инвариантность формы первого дифференциала. Непрерывность дифференцируемой функции.

Главная часть приращения функции в точке x, линейная относительно , называется дифференциалом функции в этой точке. Для обозначения дифференциала используется обозначение , а поскольку , то

.

Формула ниже позволяет вычислить приближенное значение функции, соответствующее приращенному значению аргумента, если известно ее значение в некоторой точке и значение производной в этой точке, когда приращение аргумента является достаточно малым.

Инвариантность формы дифференциала

Рассмотрим сложную функцию y=f(u(x)). Пусть функции y=f(u), u=u(x) дифференцируемы, тогда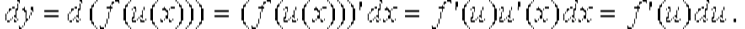

Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала, когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала

43. Теоремы Ролля, Лагранжа и Коши. Правило Лопиталя.

Теорема Ролля. Пусть функция f непрерывна на отрезке , дифференцируема на интервале и на концах отрезка принимает равные значения, то есть . Тогда существует точка , в которой .

Теорема Лагранжа. Если функция f непрерывна на отрезке 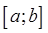, дифференцируема на интервале , то существует точка , такая, что справедлива формула:

Теорема Коши. Если функции f и g непрерывны на отрезке , дифференцируемы на интервале , причем , то существует точка , такая, что справедливо равенство

Правило Лопиталя. Пусть функции и непрерывны и дифференцируемы в окрестности точки , за исключением, быть может, точки а; и в указанной окрестности. Тогда, если существует , то существует также и , причем

44. Формула Тейлора и различные формы её остаточного члена. Основные разложения элементарных функций по формуле Тейлора.

Формула Тейлора:

Формулой Тейлора с остаточным членом в форме Лагранжа:

Ф-а Маклорена:

Разложение :

Разложение :

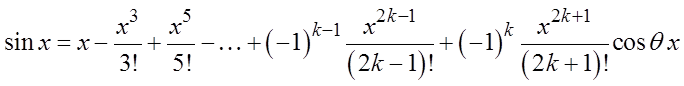
Разложение :

Разложение :

,

Дата добавления: 2015-08-21