Метод окаймляющих миноров.

Для вычисления ранга матрицы можно использовать метод окаймляющих миноров, который основывается на следующем факте: если матрица А имеет ненулевой минор порядка r и все его окаймляющие миноры равны нулю или не существуют, то ранг матрицы А равен r.

5. Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли. Формулы Крамера.

Системой m линейных алгебраических уравнений с n неизвестными 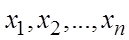называется система вида

Теорема Кронекера-Капелли. Для совместности системы линейных алгебраических уравнений необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы. Следствие 1. Если ранг матрицы системы меньше ранга ее расширенной матрицы, то система несовместна.

Пример 1. Исследовать на совместность систему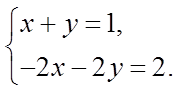

Решение. .

Имеем . Система несовместна.

Формулы Крамера:

,

где – определитель, который получается из определителя системы D путем замены j -го столбца на столбец свободных членов.

Пример 1. Решить систему

Решение. .

Дата добавления: 2015-08-21