
|
Читайте также: |
6.13. Рассмотрим экономику, состоящую из двух групп фирм: у одних цены являются гибкими, а у других – жесткими. Обозначим  - цену, устанавливаемую репрезентативной фирмой, для которой цена является гибкой, и
- цену, устанавливаемую репрезентативной фирмой, для которой цена является гибкой, и  - цену, устанавливаемую репрезентативной фирмой, для которой цена является жесткой. Фирмы с гибкими ценами устанавливают свои цены, после того как
- цену, устанавливаемую репрезентативной фирмой, для которой цена является жесткой. Фирмы с гибкими ценами устанавливают свои цены, после того как  становится известной, а фирмы с жесткими ценами - до того, как
становится известной, а фирмы с жесткими ценами - до того, как  становится известной. Таким образом, фирмы с гибкими ценами назначают
становится известной. Таким образом, фирмы с гибкими ценами назначают 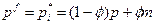 , а фирмы с жесткими ценами -
, а фирмы с жесткими ценами -  , где
, где 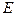 обозначает ожидаемое значение переменной в момент, когда фирмы с жесткими ценами назначают свои цены.
обозначает ожидаемое значение переменной в момент, когда фирмы с жесткими ценами назначают свои цены.
Предположим, что доля фирм с жесткими ценами составляет  , так что
, так что  .
.
(a) Выразите  через
через  ,
,  и параметры модели (
и параметры модели ( и
и  ).
).
(b) Выразите  через
через  и параметры модели.
и параметры модели.
(c) (i) Будут ли ожидаемые изменения в  оказывать влияние на
оказывать влияние на 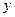 ? (Ожидаемые изменения – это изменения, о которых становится известно тогда, когда фирмы с жесткими ценами устанавливают свои цены.) Объясните свой ответ.
? (Ожидаемые изменения – это изменения, о которых становится известно тогда, когда фирмы с жесткими ценами устанавливают свои цены.) Объясните свой ответ.
(ii) Будут ли влиять неожиданные изменения в  на
на 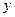 ? Объясните свой ответ.
? Объясните свой ответ.
6.14. Рассмотрим экономику, в которой в условиях несовершенной конкуренции действует большое число фирм, устанавливающих цены. Прибыль репрезентативной фирмы 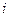 зависит от агрегированного выпуска,
зависит от агрегированного выпуска, 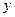 , и реальной цены фирмы,
, и реальной цены фирмы, 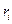 :
:  , где
, где 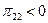 (индексы обозначают соответствующие частные производные). Обозначим
(индексы обозначают соответствующие частные производные). Обозначим  - реальная цена, доставляющая максимум прибыли фирмы. При этом
- реальная цена, доставляющая максимум прибыли фирмы. При этом  , как функция от
, как функция от 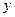 , определяется условием
, определяется условием  .
.
Предположим, что выпуск находится на некотором уровне  , и реальная цена
, и реальная цена 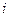 -ой фирмы равна
-ой фирмы равна 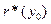 . Происходит изменение предложения денег, и при этом остальные фирмы не меняют свои цены, так что агрегированный выпуск изменяется и устанавливается на новом уровне
. Происходит изменение предложения денег, и при этом остальные фирмы не меняют свои цены, так что агрегированный выпуск изменяется и устанавливается на новом уровне  .
.
(a) Объясните, почему стимул для 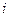 -ой фирмы подстроить свою цену задается как
-ой фирмы подстроить свою цену задается как 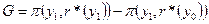 .
.
(b) Рассматривая данное выражение как функцию от  , разложите его в ряд Тейлора до второго члена в окрестности
, разложите его в ряд Тейлора до второго члена в окрестности 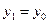 . Покажите, что
. Покажите, что  .
.
(c) Какой из элементов этого выражения характеризует степень реальной жесткости? Какой из элементов этого выражения соответствует степени нечувствительности прибыли?
6.15. Множество равновесий в модели с издержками меню. (На основе Ball and D. Romer, 1991.) Рассмотрим экономику, в которой в условиях несовершенной конкуренции действует большое число фирм. Потери в прибыли фирмы, по сравнению с ценообразованием  , составляют
, составляют  . Как обычно,
. Как обычно, 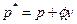 и
и 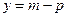 . Каждая фирма несет фиксированные издержки подстройки номинальных цен равные
. Каждая фирма несет фиксированные издержки подстройки номинальных цен равные 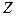 .
.
Первоначально  равна 0 и экономика находится в равновесии с гибкими ценами, в котором
равна 0 и экономика находится в равновесии с гибкими ценами, в котором 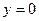 и
и  . Теперь предположим, что
. Теперь предположим, что  изменяется до
изменяется до  .
.
(a) Предположим, что доля фирм  изменила свои цены. Таким образом, фирмы, которые изменили цены, назначили
изменила свои цены. Таким образом, фирмы, которые изменили цены, назначили  , а остальные оставили их на уровне 0. Следовательно,
, а остальные оставили их на уровне 0. Следовательно,  . Используя этот факт, найдите
. Используя этот факт, найдите  ,
, 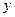 и
и  как функции от
как функции от  и
и  .
.
(b) Постройте график зависимости стимула фирмы подстраивать цену,  , от величины
, от величины  . Рассмотрите два случая:
. Рассмотрите два случая: 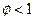 и
и 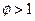 .
.
(c) Фирма подстраивает свою цену в случае, если выгоды превышают 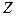 , не подстраивает, если выгоды ниже
, не подстраивает, если выгоды ниже 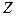 , и фирме безразлично подстраивать цену или нет, если выгоды равны
, и фирме безразлично подстраивать цену или нет, если выгоды равны 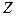 . Учитывая этот факт, возможна ли ситуация, в которой оба исхода являются равновесными: и исход, когда все фирмы принимают решение подстраивать цены, и исход, когда ни одна из фирм не подстраивает цены? Возможна ли ситуация, когда оба исхода не будут равновесными?
. Учитывая этот факт, возможна ли ситуация, в которой оба исхода являются равновесными: и исход, когда все фирмы принимают решение подстраивать цены, и исход, когда ни одна из фирм не подстраивает цены? Возможна ли ситуация, когда оба исхода не будут равновесными?
6.16. (На основе Diamond, 1982.)[43] Рассмотрим остров, заселенный  людьми, на котором растет большое число пальм. Каждый человек может находиться в одном из двух состояний: либо он не несет кокос и ищет пальму (состояние Р), либо он несет кокос и ищет другого человека с кокосом (состояние С). Если человек без кокоса находит пальму, то он забирается на нее и срывает кокос, что соответствует издержкам в размере
людьми, на котором растет большое число пальм. Каждый человек может находиться в одном из двух состояний: либо он не несет кокос и ищет пальму (состояние Р), либо он несет кокос и ищет другого человека с кокосом (состояние С). Если человек без кокоса находит пальму, то он забирается на нее и срывает кокос, что соответствует издержкам в размере 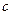 (в единицах полезности). Если человек с кокосом встречает другого человека с кокосом, то они торгуются и съедают кокосы друг друга; это приносит каждому полезность размером
(в единицах полезности). Если человек с кокосом встречает другого человека с кокосом, то они торгуются и съедают кокосы друг друга; это приносит каждому полезность размером 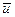 . (Люди не могут есть кокосы, сорванные ими лично.)
. (Люди не могут есть кокосы, сорванные ими лично.)
Человек, ищущий кокосы, находит пальмы с вероятностью  в единицу времени. Индивид, ищущий других обладателей кокосов, находит их с вероятностью
в единицу времени. Индивид, ищущий других обладателей кокосов, находит их с вероятностью  в единицу времени, где
в единицу времени, где 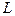 - общая численность людей, обладающих кокосом. Константы
- общая численность людей, обладающих кокосом. Константы 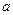 и
и  заданы экзогенно.
заданы экзогенно.
Норма дисконтирования для индивидов составляет 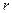 . Рассмотрим только стационарные состояния и предположим, что
. Рассмотрим только стационарные состояния и предположим, что  является константой.
является константой.
(a) Объясните, почему в случае, когда все находящиеся в состоянии Р залезают на пальму, как только ее находят, будет соблюдаться условие  , где
, где 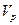 и
и 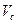 - ценность пребывания в соответствующем состоянии.
- ценность пребывания в соответствующем состоянии.
(b) Найдите аналогичное выражение для 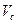 .
.
(c) Найдите выражения для 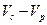 ,
, 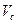 и
и 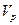 через
через 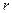 ,
,  ,
, 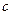 ,
, 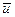 ,
, 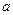 и
и 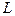 .
.
(d) Каково значение 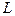 , если предположение о том, что все находящиеся в состоянии Р залезают на пальму, как только ее находят, остается в силе? Для простоты предположим, что
, если предположение о том, что все находящиеся в состоянии Р залезают на пальму, как только ее находят, остается в силе? Для простоты предположим, что  .
.
(e) Для каких значений 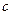 ситуация, когда все находящиеся в состоянии Р залезают на пальму, как только ее находят, является стационарной? (В предположении, что
ситуация, когда все находящиеся в состоянии Р залезают на пальму, как только ее находят, является стационарной? (В предположении, что  .)
.)
(f) Для каких значений 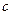 ситуация, когда никто в состояние
ситуация, когда никто в состояние  не залезет на пальму, если ее найдет, является стационарной? Существуют ли значения
не залезет на пальму, если ее найдет, является стационарной? Существуют ли значения 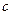 , для которых существует более одного стационарного состояния? Если существует множество равновесий, будет ли в одном из равновесий достигаться более высокое благосостояние, чем в другом? Дайте интуитивное объяснение.
, для которых существует более одного стационарного состояния? Если существует множество равновесий, будет ли в одном из равновесий достигаться более высокое благосостояние, чем в другом? Дайте интуитивное объяснение.
[1]Т.е., логарифм совокупного спроса на благо 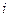 равен
равен 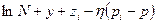 , где
, где  - численность производителей каждого блага.
- численность производителей каждого блага.
[2]Несмотря на простую интуицию, стоящую за соотношениями (6.7)-(6.9), вывод функций этого вида из задачи индивидуальной оптимизации требует определенных допущений. Сложность состоит в следующем. Если предпочтения таковы, что функция спроса на каждый товар имеет вид (6.7) при постоянной эластичности, то логарифм индекса цен будет равен среднему  только в частном случае, когда
только в частном случае, когда  . См. задачу 6.2. Данное соображение не влияет существенно на основные результаты модели.
. См. задачу 6.2. Данное соображение не влияет существенно на основные результаты модели.
[3] То, что равновесный логарифм выпуска равен 0, означает, что равновесный уровень выпуска равен 1. Это значение получается благодаря коэффициенту 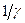 , стоящему перед
, стоящему перед  в функции полезности (6.2).
в функции полезности (6.2).
[4] Если бы индивиду были известны цены других товаров, которые он покупает, он мог бы вывести значение 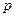 , а значит и
, а значит и  . Данную ситуацию можно исключить из рассмотрения по разным соображениям. Например, можно предположить, что домохозяйства состоят из двух индивидов, «производителя» и «покупателя», и что передача информации между ними ограничена. В оригинальной модели Лукаса экономика представлена структурой перекрывающихся поколений, где индивиды производят в первом периоде жизни и совершают покупки во втором периоде, что также позволяет обойти стороной данную проблему.
. Данную ситуацию можно исключить из рассмотрения по разным соображениям. Например, можно предположить, что домохозяйства состоят из двух индивидов, «производителя» и «покупателя», и что передача информации между ними ограничена. В оригинальной модели Лукаса экономика представлена структурой перекрывающихся поколений, где индивиды производят в первом периоде жизни и совершают покупки во втором периоде, что также позволяет обойти стороной данную проблему.
* Разумеется, речь идет об условном математическом ожидании (прим. науч. ред.).
[5] Рассматриваемая проблема построения условных ожиданий часто называется проблемой выделения сигнала. Случайная величина, наблюдаемая индивидом,  , равна сумме сигнала,
, равна сумме сигнала,  , и шума,
, и шума, 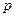 . Уравнение (6.19) представляет лучший способ получения индивидом оценки сигнала из наблюдений
. Уравнение (6.19) представляет лучший способ получения индивидом оценки сигнала из наблюдений  . Отношение
. Отношение 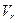 к
к 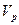 известно как отношение сигнал-шум.
известно как отношение сигнал-шум.
[6] Большая исследовательская работа, начатая в статьях Barro (1977a, 1978) и значительно продвинутая в статьях Mishkin (1982, 1983), была направлена на проверку предсказаний модели Лукаса относительно воздействий наблюдаемой и ненаблюдаемой монетарной политики, с использованием денежной массы как измерителя политики. В понимании Барро, основная идея состояла в построении регрессии выпуска на измерители предсказуемой и непредсказуемой компонент темпа роста денежной массы и некоторый набор переменных управления. К сожалению, данные тесты обладали теми же недостатками, что и регрессии выпуска на денежную массу (см. раздел 5.5). Так, например, положительная корреляция между неожиданными изменениями в денежной массе и изменениями выпуска может отражать воздействие выпуска на спрос на деньги, а не воздействие денег на выпуск. Аналогичным образом, отсутствие взаимосвязи между предсказуемыми изменениями в денежной массе и изменениями выпуска может объясняться вовсе не тем, что наблюдаемые монетарные изменения не обладают реальными эффектами, а тем, что Федеральная Резервная Система подстраивает предложение денег так, чтобы нейтрализовать воздействие прочих факторов на выпуск. См., также, задачу 6.3.
[7] Кроме того, из модели следует, что отклонения выпуска от равновесия с гибкими ценами вовсе не являются персистентными. Действительно,  зависит только от
зависит только от 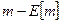 . А по определению
. А по определению 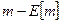 не может содержать в себе предсказуемую компоненту. Таким образом, из модели следует, что
не может содержать в себе предсказуемую компоненту. Таким образом, из модели следует, что  - это белый шум, который, естественно, не характеризуется ни положительной, ни отрицательной корреляцией во времени (автокорреляцией – прим. перев.). Но это не совсем соответствует экономической реальности. Так, ограничительная политика Федеральной Резервной Системы в 1979 году, направленная на снижение инфляции, привела к ненормально низкому объему выпуска на протяжении достаточно продолжительного периода времени, а вовсе не на протяжении лишь одного периода, с последующим возвратом выпуска к нормальному уровню.
- это белый шум, который, естественно, не характеризуется ни положительной, ни отрицательной корреляцией во времени (автокорреляцией – прим. перев.). Но это не совсем соответствует экономической реальности. Так, ограничительная политика Федеральной Резервной Системы в 1979 году, направленная на снижение инфляции, привела к ненормально низкому объему выпуска на протяжении достаточно продолжительного периода времени, а вовсе не на протяжении лишь одного периода, с последующим возвратом выпуска к нормальному уровню.
Данное затруднение может быть разрешено, если предположить, что первоначальная реакция выпуска на ненаблюдаемый монетарный шок активизирует некоторые процессы, которые не позволяют вернуться выпуску к нормальному уровню даже после того, как шок был идентифицирован. Примерами подобных механизмов является динамика товарно-материальных запасов (Blinder and Fischer, 1981), накопление капитала (Lucas, 1975) и единовременные издержки поиска и обучения новых работников. Таким образом, предсказание, что выпуск будет следовать процессу случайного блуждания, является скорее артефактом, вытекающим из упрощенной формы рассмотренной модели, а вовсе не устойчивым следствием.
[8] Важной ранней работой является Akerlof (1969). См. также Phelps (1978) и Blanchard (1983).
[9] Все три модели строятся на предположении о постепенной подстройке цен. Но, по крайней мере, для моделей Фишера и Тейлора, если время пересмотра цен сделать эндогенным, в результате получится синхронная, а вовсе не постепенная подстройка цен (см. задачу 6.8). Постепенный характер подстройки может возникнуть эндогенным образом, если предположить, что фирмы желают получить информацию о ценах других фирм до устанавления собственных цен (Ball and Cecchetti, 1988). Также это возможно в случае существования специфичных для фирм шоков (Ball and D. Romer, 1989; Caballero and Engel, 1991), и в случае стратегического взаимодействия фирм (Maskin and Tirole, 1988).
[10] Отсутствие общеэкономического рынка труда является важной чертой модели Лукаса. Если бы данный рынок присутствовал в модели, индивиды на основе наблюдаемой номинальной заработной платы могли бы раскрыть информацию о предложении денег, что сделало бы нейтральными любые номинальные шоки. Напротив, введение конкурентного рынка труда в данную модель не является критичным для получаемых результатов.
[11] Как обсуждается в сноске 2 и в задаче 6.2, в случае, когда предпочтения индивидов относительно различных товаров заданы так, что кривая спроса на каждый товар обладает постоянной эластичностью, аккуратное определение (логарифмов) индексов цен и выпуска является более сложным, чем простое среднее арифметическое по  и
и 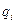 . В задаче 6.4 требуется показать, что основные результаты, полученные в данном разделе, не претерпевают существенных изменений в случае использования точных индексов.
. В задаче 6.4 требуется показать, что основные результаты, полученные в данном разделе, не претерпевают существенных изменений в случае использования точных индексов.
[12] Оригинальные версии данных моделей рассматривают постепенную подстройку ставок заработной платы. Цены являются гибкими, но определяются по принципу наценки над заработной платой. Для простоты, мы рассматриваем непосредственно постепенную подстройку цен. Это не влияет на основные выводы модели.
[13] В работе Haltiwanger and Waldman (1989) показывается в общем случае, как небольшая доля агентов, не реагирующих на шоки, может оказывать непропорционально большой эффект на экономику.
[14] Т.к.  и
и  , мы можем представить все переменные в уравнении (6.75) как ожидания, формируемые в момент времени
, мы можем представить все переменные в уравнении (6.75) как ожидания, формируемые в момент времени 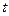 . Таким образом, в последующем анализе, лаговый оператор всегда можно рассматривать как оператор, сохраняющий все переменные как ожидания в период времени
. Таким образом, в последующем анализе, лаговый оператор всегда можно рассматривать как оператор, сохраняющий все переменные как ожидания в период времени 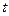 . Оператор обратного сдвига,
. Оператор обратного сдвига, 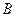 , используется для обозначения функции, которая переносит назад как индекс времени переменной, так и индекс времени ожиданий. Например,
, используется для обозначения функции, которая переносит назад как индекс времени переменной, так и индекс времени ожиданий. Например, 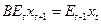 . Удобнее ли использовать лаговый оператор или оператор обратного сдвига – зависит от конкретной ситуации. В данном случае удобнее использовать лаговый оператор.
. Удобнее ли использовать лаговый оператор или оператор обратного сдвига – зависит от конкретной ситуации. В данном случае удобнее использовать лаговый оператор.
[15] Т.к. оператор 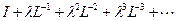 представлен бесконечной суммой, требуется существование предела
представлен бесконечной суммой, требуется существование предела 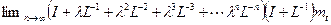 . Это в свою очередь требует, чтобы член
. Это в свою очередь требует, чтобы член 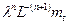 (равный
(равный 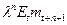 ) стремился к нулю. В случае, когда
) стремился к нулю. В случае, когда  (т.е.
(т.е.  ), и когда
), и когда  следует процессу случайного блуждания, данное условие соблюдается.
следует процессу случайного блуждания, данное условие соблюдается.
[16] Причина, по которой мы не можем записать (6.82) для 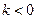 состоит в том, что закон итерированных проекций не может быть назад-смотрящим: текущие ожидания относительно ожиданий, сформированных когда-то в прошлом относительно некой переменной, вовсе не обязаны совпадать с текущими ожиданиями переменной.
состоит в том, что закон итерированных проекций не может быть назад-смотрящим: текущие ожидания относительно ожиданий, сформированных когда-то в прошлом относительно некой переменной, вовсе не обязаны совпадать с текущими ожиданиями переменной.
[17] Более обстоятельное введение в технику лаговых операторов можно найти в книге Sargent (1987a, глава 9).
[18] Используя (6.84) и то, что  , можно вывести уравнение динамики инфляции, аналогичное (6.86):
, можно вывести уравнение динамики инфляции, аналогичное (6.86): 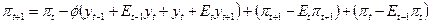 . Здесь
. Здесь  также присутствует с отрицательным знаком.
также присутствует с отрицательным знаком.
[19] Есть еще один способ показать, что модель Тейлора демонстрирует инерцию динамики уровня цен, но не инерцию инфляции. Для этого нужно рассмотреть общее решение модели (6.80), когда агрегированный спрос не содержит в себе компоненту, определяемую процессом случайного блуждания. Пусть экономика первоначально находится в состоянии равновесия с гибкими ценами и инфляция стационарна. Рассмотрим последствия двух возможных изменений в политике. В первом случае, происходит однопериодное сокращение темпа роста денежной массы, после чего он возвращается к первоначальному значению. Во втором случае, происходит перманентное снижение темпа роста денежной массы. В соответствии с уравнением (6.80), устанавливаемые индивидами цены определяются всей ожидаемой в будущем траекторией денежной массы. Перманентное снижение темпа роста денежной массы в большей степени сократит ожидаемые в будущем объемы денежной массы, по сравнению с временным снижением темпа роста денежной массы. В результате, перманентное изменение темпа роста денежной массы в большей степени будет воздействовать на вновь устанавливаемые цены, по сравнению с временным изменением.
[20] Кроме того, данный результат помогает обосновать предположение, что первоначальное распределение величины  является равномерным на интервале от
является равномерным на интервале от  до
до  . Для каждого индивида
. Для каждого индивида  пробегает все значения на интервале от
пробегает все значения на интервале от  до
до  в промежутке между двумя моментами подстройки цен. Так что нет никаких оснований предполагать возможность концентрации цен где-либо на интервале. Действительно, Кэплин и Спалбер показали, что в простых предположениях, величина
в промежутке между двумя моментами подстройки цен. Так что нет никаких оснований предполагать возможность концентрации цен где-либо на интервале. Действительно, Кэплин и Спалбер показали, что в простых предположениях, величина  у данного индивида равновероятно может принимать любое значение на интервале от
у данного индивида равновероятно может принимать любое значение на интервале от  до
до  .
.
[21] Более обстоятельный анализ данных проблем можно найти в работах Caballero and Engel (1991, 1993).
[22] Местами, материал в разделе 6.9 заимствован из работы D. Romer (1993).
[23] Основополагающими работами являются Mankiw (1985) и Akerlof and Yellen (1985). См. также Parkin (1986), Rotemberg (1982) и Blanchard and Kiyotaki (1987).
[24] Условие, когда подстройка всеми фирмами своих цен является равновесной ситуацией, вовсе не формулируется просто с точностью до наоборот. В результате, возможно, что равновесными будут одновременно и ситуация всеобщей подстройки цен, и ситуация неизменных цен. См. задачу 6.15.
[25] Падение агрегированного выпуска, скорее всего, приведет к снижению заработной платы, что сдвинет кривую предельных издержек вниз. В целях упрощения анализа, данный эффект не отображен на диаграмме.
[26] Несмотря на то, что величина  является чувствительной к параметрам
является чувствительной к параметрам 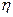 и
и 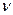 , ни для каких разумных значений параметров выигрыш фирмы от подстройки цены не окажется маленьким. Возьмем, например,
, ни для каких разумных значений параметров выигрыш фирмы от подстройки цены не окажется маленьким. Возьмем, например, 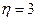 (при этом наценка будет составлять 50%) и
(при этом наценка будет составлять 50%) и  . Даже для таких пограничных значений параметров выигрыш от подстройки цен будет равен 0.8% от уровня равновесной выручки для 3% снижения выпуска, и 2.4% для 5% снижения выпуска. Хотя эти значения намного ниже тех, что были получены в базовом примере, они все равно намного выше издержек подстройки цен в типичной ситуации.
. Даже для таких пограничных значений параметров выигрыш от подстройки цен будет равен 0.8% от уровня равновесной выручки для 3% снижения выпуска, и 2.4% для 5% снижения выпуска. Хотя эти значения намного ниже тех, что были получены в базовом примере, они все равно намного выше издержек подстройки цен в типичной ситуации.
[27] Проблему нельзя обойти, предположив, что издержки подстройки возникают не при изменении цены, а при изменении заработной платы. В данном случае стимул снизить цену действительно будет низким. Однако стимул сократить заработную плату будет велик: фирмы, которые имеют возможность снизить издержки на труд, и работники, которые имеют возможность увеличить количество часов работы, будут оказывать давление на заработную плату в сторону ее снижения.
[28] Это вытекает из предположения, что максимизирующая прибыль относительная цена является возрастающей функцией агрегированного выпуска. Т.е., это соответствует предпосылке 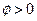 в уравнении ценообразования (6.45). Как обсуждалось в разделе 6.4, данное условие необходимо для того, что равновесие с гибкими ценами являлось устойчивым.
в уравнении ценообразования (6.45). Как обсуждалось в разделе 6.4, данное условие необходимо для того, что равновесие с гибкими ценами являлось устойчивым.
[29] Данная аналогия впервые была предложена в работе Friedman (1953, стр. 173), в контексте анализа обменных курсов.
[30] Для простоты на Рис. 6.3 не отражен сдвиг кривой предельных издержек (см. сноску 25). Однако в общем случае кривая, конечно же, сдвигается.
[31] Классической здесь является работа Diamond (1982). См. также Caballero and Lyons (1992); Cooper and Haltiwanger (1996); и Basu and Fernald (1995).
[32] Как обсуждалось в разделе 5.3, в действительности наценки являются в лучшем случае умеренно контрциклическими. Если это происходит потому, что оптимальные наценки фирм являются контрциклическими, то можно говорить о реальной жесткости с точки зрения выручки фирм. Однако это будет не так, если наценки являются контрциклическими только потому, что существуют препятствия на пути подстройки номинальных цен, которые вынуждают фирмы не подстраивать свои цены в ответ на проциклические колебания предельных издержек (см. Sbordone, 1998).
[33] Кроме того, возможность высокой степени реальной жесткости на рынке труда предполагает, что незначительные препятствия на пути номинальной подстройки могут породить серьезные реальные эффекты номинальных шоков даже в том случае, когда жесткими являются не номинальные цены, а номинальная заработная плата. Если заработная плата обладает высокой степени реальной жесткости, рост спроса приведет лишь к слабому росту оптимальной реальной заработной платы. В результате, так же как небольшие трения в процессе подстройки номинальных цен часто порождают серьезную жесткость номинальных цен, незначительные трения в процессе подстройки номинальной заработной платы могут породить существенную жесткость номинальной заработной платы.
[34] Если цены являются гибкими, то каждая фирма устанавливает свою относительную цену на уровне 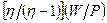 . При этом в равновесии с гибкими ценами реальная заработная плата должна быть равна
. При этом в равновесии с гибкими ценами реальная заработная плата должна быть равна 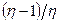 , и объем предложения труда при этом будет равен
, и объем предложения труда при этом будет равен  . Тогда условие, что в равновесии с гибкими ценами объем предложения труда превосходит объем спроса на труд, имеет вид:
. Тогда условие, что в равновесии с гибкими ценами объем предложения труда превосходит объем спроса на труд, имеет вид:  .
.
[35] Данный термин ввел Ирвинг Фишер (Fisher, 1933). См. также современный анализ Bernanke and Gertler (1989). В разделе 8.7 представлена модель инвестиций в условиях несовершенства финансового рынка, где рассматривается эффект изменения богатства предпринимателя.
[36] Если незначительное снижение богатства должника резко снижает его возможность заимствовать, то увеличение издержек уже не будет малым (см., например, Mankiw, 1986a, и Bernanke and Gertler, 1990). Однако не совсем ясно, почему небольшое снижение богатства должника заставляет кредитора прекратить финансирование, если, например, в то же самое время происходит значительное снижение издержек на труд. Также не ясно, почему небольшое перераспределение должно оказывать значительный эффект на число предпринимателей, имеющих возможность брать в долг.
[37] Существует еще одно направление исследований. В каждый момент времени далеко не все агенты подстраивают свой запас денежной базы. Так что в ситуации, когда монетарная политика изменяет общий объем денежной базы, она не может добиться пропорционального увеличения запасов каждого агента. В результате, изменение денежной базы в общем случае влияет на реальные денежные остатки, даже если все цены и ставки заработной платы являются полностью гибкими. При определенных условиях (например, если реальные денежные остатки влияют на потребление) данное изменение в реальных денежных остатках воздействует на реальную ставку процента. И если реальная ставка процента влияет на агрегированное предложение, то в результате может произойти изменение в агрегированном выпуске. См. основополагающие работы Grossman and Weiss (1983) и Rotemberg (1984), а также современную дискуссию в работе Christiano, Eichenbaum and Evans (1997).
[38] Однако, отсутствие видимой взаимосвязи между  и
и  является загадкой не только для модели Лукаса, но и для моделей основанных на небольших фрикциях. Действительно, рост дисперсии шоков должен заставлять фирмы менять цены чаще, а следовательно, должен снизить реальное воздействие шоков агрегированного спроса.
является загадкой не только для модели Лукаса, но и для моделей основанных на небольших фрикциях. Действительно, рост дисперсии шоков должен заставлять фирмы менять цены чаще, а следовательно, должен снизить реальное воздействие шоков агрегированного спроса.
[39] Можно говорить о равновесии, определяемом пятнами на солнце, в ситуации, когда переменная, которая не должна оказывать воздействие на экономику, становится значимой только потому, что экономические агенты верят в это. Любые модели с множеством равновесий потенциально связаны с этой проблемой: если агенты верят в то, что экономика придет в одно равновесие, когда некая посторонняя переменная принимает высокое значение, и в другое равновесие, когда эта переменная имеет низкой значение, то их поведение и определит соответствующий окончательный исход. Подробнее см. Cass and Shell (1983), Woodford (1990, 1991), Benhabib and Farmer (1999).
[40] При этом не существует однозначной взаимосвязи между наклоном функции реакции и уровнем благосостояния, достигаемым в различных состояниях равновесия. Если задача индивидуальной оптимизации имеет внутреннее решение, то  определяется из условия
определяется из условия  , где нижний индекс обозначает соответствующую частную производную. Дифференцируя данное уравнение по
, где нижний индекс обозначает соответствующую частную производную. Дифференцируя данное уравнение по  , получаем:
, получаем:  . Для того чтобы
. Для того чтобы  было внутренним максимумом,
было внутренним максимумом, 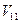 должно быть меньше нуля. Следовательно, знак
должно быть меньше нуля. Следовательно, знак  определяется знаком
определяется знаком  . С другой стороны, относительный уровень благосостояния в различных состояниях равновесия определяется величиной
. С другой стороны, относительный уровень благосостояния в различных состояниях равновесия определяется величиной  . Таким образом, существует ли множество равновесий, и является ли равновесие с высоким выпуском предпочтительным по сравнению с равновесием с низким выпуском – это разные вопросы.
. Таким образом, существует ли множество равновесий, и является ли равновесие с высоким выпуском предпочтительным по сравнению с равновесием с низким выпуском – это разные вопросы.
[41] Кроме того, они добавили к функции выигрышей константу $0.60, так что никто из агентов не может потерять деньги.
[42] Если мы берем за основу предположение о высокой степени реальной жесткости, то это вовсе не означает, что мы соглашаемся с важностью многих шоков. В рассмотренном примере с переходом на летнее время, несмотря на высокую степень реальной жесткости в индивидуальных предпочтениях относительно личных расписаний, мы вовсе не наблюдаем краткосрочных изменений в общем реальном расписании, возникающих по причинам отличным от изменений в стандарте времени. И, наконец, существует промежуточная ситуация, когда в условиях высокой степени реальной жесткости не только реальные, но и номинальные шоки имеют значений (см., например, Greenwald and Stiglitz, 1988).
[43] Решение этой задачи требует использования метода динамического программирования (см. раздел 9.4).
Дата добавления: 2015-10-30; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Но хрупкое равновесие | | | Цепочка развития ТС |