Эмпирические приложения

Средний уровень инфляции и проблема выбора между выпуском и инфляцией

В работе Ball, Mankiw and D. Romer (1988) отмечается, что если реальные эффекты шоков агрегированного спроса обусловлены фрикциями в подстройке цен, то величина данных эффектов, скорее всего, должна быть связана со средним уровнем инфляции. Приводится следующий простой аргумент. Чем выше средний уровень инфляции, тем чаще фирмы вынуждены подстраивать свои цены вслед за изменением уровня цен. Следовательно, они быстрее реагируют на шоки, и их реальные эффекты будут слабее.

Тест данной гипотезы, проводимый Болом, Менкью и Ромером, аналогичен тесту Лукаса на наличие взаимосвязи между дисперсией агрегированного спроса и реальными эффектами шоков спроса. Следуя Лукасу, авторы вначале строят оценку реального воздействия шоков спроса (обозначенную за ), используя широкую выборку по странам и спецификацию (6.34). Затем они проверяют, как полученная оценка связана со средним уровнем инфляции.

На Рис. 6.5 представлена корреляционная диаграмма для оценки и среднего уровня инфляции по 43 странам, включенным Болом, Менкью и Ромером в выборку. Как видно из диаграммы, зависимость является отрицательной. Соответствующая регрессия (с дополнительным квадратным членом, учитывающим явно наблюдаемую нелинейность) имеет вид:

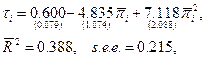(6.95)

где 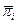- средний уровень инфляции в стране 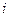, а величины в скобках – стандартные ошибки. Точечная оценка означает, что 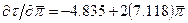, что будет меньше нуля для 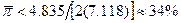. Таким образом, выявлена статистически значимая отрицательная взаимосвязь между средним уровнем инфляции и построенной оценкой реального воздействия шоков агрегированного спроса.

Средний уровень инфляции

Рис. 6.5. Проблема выбора между выпуском и инфляцией

и средний уровень инфляции (из статьи Ball, Mankiw and Romer, 1988)

Как мы помним, модель Лукаса предсказывает, что дисперсия шоков агрегированного спроса влияет на 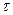, и это подтверждается статистикой. Более того, страны с более высоким средним уровнем инфляции, как правило, характеризуются большей дисперсией шоков агрегированного спроса. Так что, возможно, результат, полученный в (6.95), имеет место не потому, что 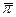непосредственно влияет на 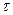, а потому, что средний уровень инфляции коррелирован со стандартным отклонением темпа роста номинального ВНП (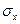), который оказывает непосредственное воздействие на 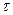. 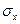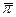Но возможна и противоположная ситуация, когда результат тестирования подтверждает гипотезу Лукаса просто потому, что и - коррелированны.

Чтобы проверить, какая из этих двух гипотез является справедливой, следует включить обе переменные в регрессию. Опять же, учитывая явную нелинейность, имеет смысл включить также и квадратные члены.

(6.96)

Коэффициенты перед показателями средней инфляции существенно не изменились по сравнению с предшествующей регрессией и остались статистически значимыми. Напротив, показатели отклонения играют незначительную роль. Нулевая гипотеза, что коэффициенты перед 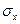и 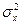равны нулю, не может быть отвергнута на любом разумном доверительном интервале. И точечная оценка говорит о том, что разумные изменения 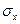оказывают количественно слабое воздействие на 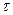. Например, изменение 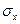с 0.05 до 0.10 изменяет 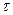на 0.04. Таким образом, результаты говорят в пользу новой кейнсианской теории, а не модели Лукаса.[38]

Работа Kiley (2000) продолжает анализ, дополнительно учитывая характер персистентности колебаний выпуска. Вначале он отмечает, что из новых кейнсианских моделей следует, что отклонения выпуска от нормального уровня носят менее персистентный характер в случаях, когда средний уровень инфляции является относительно высоким. Здесь снова можно говорить о том, что для более высокой средней инфляции частота подстройки цен должна быть выше. Следовательно, экономика быстрее будет возвращаться к равновесию с гибкими ценами после шока. Статистика подтверждает данную гипотезу.

Дата добавления: 2015-10-30