Модель Кэплина-Спалбера

В моделях Фишера и Тейлора предполагалось, что моменты подстройки цен определяются сугубо течением времени. Это неплохое приближение для заработной платы, определяемой в коллективном договоре или заработной платы, назначаемой ежегодно, а также для цен в каталогах. Но во многих других случаях, данный принцип не дает адекватного описания действительности. Например, магазины розничной торговли могут свободно выбирать моменты изменения своих цен в зависимости от положения дел в экономике. Поэтому важно исследовать последствия ценообразования, определяемого состоянием. В качестве примера мы разберем модель Кэплина-Спалбера.

Модель строится в непрерывном времени. Оптимальная цена каждого индивида в момент времени , , 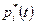также как и раньше определяется выражением . Темп роста денежной массы всегда положителен. Как мы увидим, это приводит к тому, что постоянно возрастает. Основное предположение модели состоит в том, что индивиды, устанавливающие цены, следуют при этом -ценовой политике. А именно, в любой момент, когда индивид подстраивает свою цену, он устанавливает ее таким образом, чтобы разрыв между фактической ценой и оптимальной ценой в этот момент времени, , соответствовал целевому уровню . После чего, индивид не меняет цену до тех пор, пока рост денежной массы не увеличит настолько, что разрыв опустится ниже определенного спускового уровня . Тогда индивид снова переустанавливает до уровня , и процесс продолжается дальше.

политика подобного рода является оптимальной в ситуации, когда инфляция стационарна, агрегированный выпуск не меняется, и существуют фиксированные издержки изменения номинальных цен (Barro, 1972; Sheshinski and Weiss, 1977). Кэплин и Спалбер приводят еще ряд примеров, когда такая политика является оптимальной, даже если выпуск и инфляция не являются постоянными. Но даже в случаях, когда политика не является полностью оптимальной, она дает простой и удобный пример определяемого состоянием ценообразования.

Необходимо ввести еще два предположения технического характера. Во-первых, для того чтобы избежать ситуации перелета ценами границы , и чтобы исключить концентрацию в распределении цен среди индивидов, мы будем предполагать, что изменяется непрерывно. Во-вторых, первоначальное распределение цен среди производителей полагается равномерным на интервале от до . Остальные предположения - такие же, как и в моделях Фишера и Тейлора.

Во введенных предположениях деньги являются нейтральными на агрегированном уровне, несмотря на негибкость цен на индивидуальном уровне. Чтобы доказать это, рассмотрим увеличение на величину на протяжении некоторого периода времени. Наша задача – найти соответствующие изменения уровня цен и выпуска, и 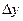. Т.к. , то увеличение оптимальной цены каждого индивида составит . Индивиды подстраивают цены только тогда, когда опускается ниже . Таким образом, цены будут менять те индивиды, у которых первоначально величина была ниже, чем . Далее, коль скоро первоначальная величина распределена равномерно на интервале от до , то это означает, что доля индивидов, которые будут подстраивать свои цены, составит . Каждый индивид, который на протяжении рассматриваемого периода времени меняет свою цену, делает это в тот момент, когда его собственный показатель достигает . Так что каждый индивид подстраивает цену ровно на величину . Объединяя все эти соображения вместе, получаем что:

(6.87)

Из (6.87) следует, что 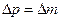, а значит . Таким образом, изменение в денежной массе действительно не оказывает воздействия на агрегированный выпуск.[20]

Еще проще понять этот результат, если рассмотреть частный случай , так что просто равно 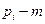. Окружность, изображенная на Рис. 6.2 помогает представить распределение точек на интервале . Первоначально индивиды распределены равномерно вдоль окружности. Увеличение на передвигает положение каждого индивида против часовой стрелки на расстояние вдоль окружности. Действительно, рассмотрим сперва индивида, находящегося в точке и имеющего первоначально величину меньше, чем . Данный индивид не будет менять свою цену при увеличении на . При этом, т.к. возрастает на , то падает на . Рассмотрим теперь индивида, находящегося в точке и характеризующегося величиной , равной , где меньше . У данного индивида величина упадет ниже критической отметки еще до того, как вырастет на величину . Так что данный индивид перемещается вдоль окружности против часовой стрелки. В момент времени, когда достигает , увеличивается скачком на , так что дискретно перемещается от к . Однако на диаграмме, это всего лишь предельно малое продвижение по окружности. Далее с ростом рассматриваемый индивид уже не будет менять цену. Его положение будет плавно перемещаться по окружности. Так что полное расстояние, на которое он переместится, также будет равно .

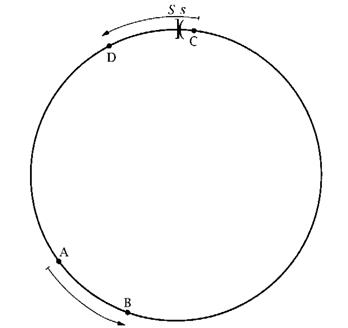
Рис. 6.2 Эффекты увеличения денежной массы в модели Кэплина-Спалбера

Т.к. все индивиды первоначально равномерно распределены вдоль окружности, и коль скоро каждый из них передвигается на одно и то же расстояние, окончательно они также будут равномерно распределены. Таким образом, распределение величины 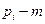остается неизменным. А т.к. 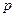определяется как среднее по , то также не изменяется.

Причина столь сильного отличия результатов данной модели и модели Тейлора состоит в природе политики подстройки цен. В модели Кэплина-Спалбера, число индивидов, меняющих цены в каждый момент времени тем выше, чем выше темп роста предложения денег. В тех предположениях, что вводят Кэплин и Спалбер, это сопровождается полной реакцией агрегированного уровня цен на изменение в . Напротив, в модели Тейлора число индивидов, меняющих свои цены, в каждый момент времени фиксировано. В результате, уровень цен не реагирует в полной мере на изменение в .

Однако нейтральность денег, возникающая в модели Кэплина-Спалбера, не является общим результатом широкого класса моделей, в которых число индивидов, меняющих цены, определяется эндогенным образом в каждый момент времени в силу наличия постоянных издержек подстройки цен. Например, если допустить, что инфляция может быть не только положительной, но и отрицательной, или ввести в модель идиосинкратические шоки, которые время от времени вынуждают индивидов снижать свои номинальные цены, то возникающие расширения правила чаще всего порождают реальные эффекты монетарных шоков (см., например, Iwai, 1981; Caplin and Leahy, 1991; и задачу 6.12). Кроме того, величины и могут меняться в ответ на шоки агрегированного спроса. Например, если высокий темп роста денежной массы сегодня сигнализирует о высоком темпе роста денежной массы в будущем, индивиды расширят границы -диапазона в ответ на положительный монетарный шок. В результате ни один индивид не приспособит свою цену в краткосрочном периоде (т.к. никто не окажется в новой, более низкой спусковой точке ), так что данный положительный шок приведет к увеличению выпуска (Tsiddon, 1991).[21]

Таким образом, модель Кэплина-Спалбера не следует рассматривать как основополагающую модель для анализа эффектов агрегированного спроса. Модель является важной по другим причинам. Во-первых, она предлагает нам пример определяемого состоянием ценообразования. Во-вторых, она выявляет новые для нас причины сложной взаимосвязи между жесткостью цен на микро и макроуровне. Модели Фишера и Тейлора показывают, что временная жесткость некоторых цен может порождать диспропорциональное воздействие шоков агрегированного спроса на агрегированный уровень цен. Напротив, модель Кэплина-Спалбера показывает, что диспропорциональный эффект может порождать как раз подстройка некоторых цен: небольшая доля индивидов, подстраивающих цены на значительную величину, вполне может породить нейтральность на агрегированном уровне. Таким образом, представленные модели Фишера, Тейлора и Кэплина-Спалбера совместно показывают, что основательный анализ жесткости цен требует пристального внимания как к природе политики подстройки цен, так и к тому, как эти политики взаимодействуют в процессе определения динамики агрегированного уровня цен.

Часть С. Новая кейнсианская экономика [22]

Модели Лукаса, Фишера и Тейлора не дают исчерпывающего объяснения реальных эффектов шоков агрегированного спроса. В основе данных моделей лежат такие несовершенства, которые в действительности не представляют особых затруднений для экономических агентов (несовершенная информация относительно уровня цен в модели Лукаса и нечастая подстройка цен и заработной платы в моделях Фишера и Тейлора). Аккуратная информация относительно динамики уровня цен является легкодоступной, и издержки перехода к более частой подстройке цен и заработной платы (например, с использованием индексации или других механизмов) являются довольно низкими. Возникает вопрос: почему экономические агенты должны позволять номинальным шокам серьезно влиять на выпуск, когда достаточно легко можно практически полностью устранить номинальные несовершенства?

Основная идея многочисленных исследований реальных эффектов, порождаемых номинальными шоками, состоит в том, что представленная проблема относится не только к рассмотренным моделям, но и ко всем потенциально возможным источникам номинальных несовершенств. Индивидов, в основном, интересуют реальные цены и объемы: реальная заработная плата, количество рабочих часов, реальный уровень потребления, и т.д. Номинальные величины играют намного меньшую роль и проблемы с ними часто легко можно обойти. Цены и ставки заработной платы определяются в номинальном исчислении, но их можно изменить или индексировать, не неся при этом больших издержек. Индивиды не обладают полной информацией относительно уровня цен, но они могут получить достаточно точные сведения за небольшую плату. Долговые контракты также, как правило, специфицируются в номинальных величинах, но опять же, они могут быть проиндексированы без особых затруднений. Индивиды хранят на руках умеренные суммы наличности, которая деноминирована в номинальных единицах, но они могут без труда их изменить. Нет никаких оснований полагать, что номинальные переменные сами по себе важны для индивидов.

Таким образом, в соответствии с новым кейнсианским взглядом, если номинальные несовершенства важны для объяснения колебаний на агрегированном уровне, то необходимо, чтобы номинальные фрикции, которые сами по себе малы на микроэкономическом уровне, каким-то образом порождали серьезные эффекты на макроэкономическом уровне. Большинство исследований в области микроэкономических обооснований номинальной жесткости посвящены именно вопросу, может ли это действительно иметь место.[23]

Для определенности, большая часть данного раздела посвящена анализу сформулированной проблемы на основе частного случая номинального несовершенства. А именно, мы будем работать со статической моделью, в которой фирма сталкивается с издержками меню­ – небольшими фиксированными издержками подстройки номинальных цен. (Стандартный пример подобной ситуации – издержки ресторана на изготовление новых меню - отсюда и название). При этом, как будет показано в конце раздела 6.9, качественно те же проблемы возникают в анализе других источников номинальной жесткости. Кроме того, анализ будет сфокусирован на вопросе, могут ли издержки меню породить существенную номинальную жесткость при реакции на временный монетарный шок. В результате, анализ в большей степени является успешным в характеристике микроэкономических условий возникновения медленной подстройки, чем в выводах относительно роли этих условий для специфики подстройки цен.

В разделе 6.8 показывается, что само по себе введение ценообразования с издержками меню в вальрасовскую (в остальных чертах) модель экономики, вероятно, не может породить существенной номинальной жесткости. Раздел 6.9, тем самым, посвящен поиску дополнительных обстоятельств, позволяющих издержкам меню иметь значительные эффекты. В разделе 6.10 представлены результаты некоторых важных эмпирических исследований. В последних разделах 6.11 и 6.12 обсуждаются некоторые расширения и ограничения теории.

---

Дата добавления: 2015-10-30