
|
Читайте также: |
Применение определенного интеграла к вычислению
площадей фигур в прямоугольной системе координат
Пусть задана функция 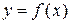 , непрерывная на отрезке
, непрерывная на отрезке  . Тогда площадь
. Тогда площадь 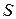 фигуры, ограниченной графиком функции
фигуры, ограниченной графиком функции 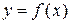 (
(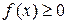 при
при 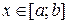 ), осью
), осью  (прямая
(прямая 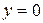 ), прямыми
), прямыми  (см. рис. 6.1) вычисляется по формуле
(см. рис. 6.1) вычисляется по формуле
 . (6.1)
. (6.1)
Если же заданы две функции  ,
, 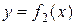 , непрерывные на отрезке
, непрерывные на отрезке  , причем на этом отрезке
, причем на этом отрезке 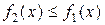 (график функции
(график функции 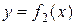 лежит ниже графика функции
лежит ниже графика функции  ), то площадь
), то площадь 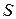 фигуры, ограниченной графиками этих функций и прямыми
фигуры, ограниченной графиками этих функций и прямыми  (см. рис. 6.2), вычисляется по формуле
(см. рис. 6.2), вычисляется по формуле
 . (6.2)
. (6.2)

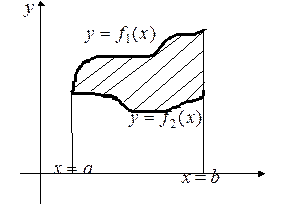
Рис. 6.1. Рис. 6.2.
Пример 1. Найти площадь фигуры, ограниченной графиком функции 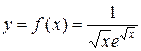 , осью
, осью  , если
, если  .
.
Решение: В данном случае необходимо применить формулу (6.1), в которой 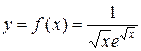 ,
,  . Итак,
. Итак,

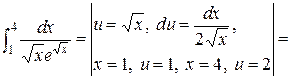
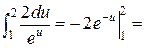
 .
.
Пример 2. Найти площадь фигуры, ограниченной графиками функций  и прямой
и прямой  .
.
Решение: Для решения задачи необходимо применить формулу (6.2). Сначала определим функции  ,
, 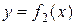 и отрезок интегрирования
и отрезок интегрирования  . Сделаем чертеж (см. рис. 6.3).
. Сделаем чертеж (см. рис. 6.3).
Из чертежа видно, что  , , 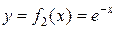 , , 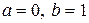 . Тогда . Тогда

| 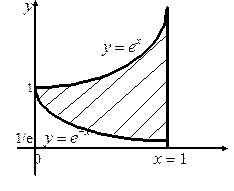 Рис. 6.3
Рис. 6.3
|
Вычисление длины дуги кривой, заданной уравнением
В прямоугольной декартовой системе координат
Пусть задана функция 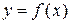 , определенная и дифференцируемая (а значит, непрерывная) на конечном отрезке
, определенная и дифференцируемая (а значит, непрерывная) на конечном отрезке  . Тогда длина
. Тогда длина 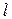 дуги кривой, определяемой уравнением
дуги кривой, определяемой уравнением 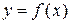 на отрезке
на отрезке  , вычисляется по формуле
, вычисляется по формуле
 . (6.3)
. (6.3)
Пример 3. Найти длину дуги кривой, уравнение которой на отрезке 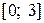 задается уравнением
задается уравнением 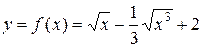 .
.
Решение: Функция 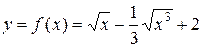 является дифференцируемой, как сумма дифференцируемых степенных функций. Вычисляя производную
является дифференцируемой, как сумма дифференцируемых степенных функций. Вычисляя производную 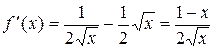 , и используя равенство (6.3), получим
, и используя равенство (6.3), получим
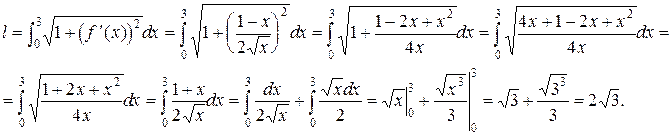
Пример 4. Найти длину дуги кривой  от
от 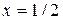 до
до  .
.
Решение: Данная функция  является дифференцируемой на отрезке
является дифференцируемой на отрезке 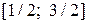 по теореме о производной сложной функции. Вычисляя производную
по теореме о производной сложной функции. Вычисляя производную 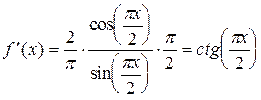 , и применяя формулу
, и применяя формулу
(6.3), получим 


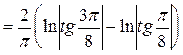 .
.
Используя формулу половинного аргумента 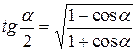 , получим
, получим  ,
,  , и окончательно,
, и окончательно, 
 .
.
Лекция 5
7. Несобственные интегралы 1-го рода
Определение 1. Если функция 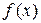 определена и непрерывна на полуинтервале
определена и непрерывна на полуинтервале  , то несобственным интегралом первого рода (интегралом с бесконечным пределом интегрирования) называют предел
, то несобственным интегралом первого рода (интегралом с бесконечным пределом интегрирования) называют предел
 . (7.1)
. (7.1)
Если существует конечный предел правой части равенства (7.1), то интеграл (7.1) сходится. Если предел правой части равен бесконечности или вообще не существует, то интеграл (7.1) расходится.
При вычислении интеграла (7.1) необходимо знать первообразную  для функции
для функции 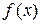 . Если ее удается найти, то
. Если ее удается найти, то  . Однако не всегда удается найти первообразную
. Однако не всегда удается найти первообразную  и тогда для установления сходимости (расходимости) интеграла (7.1) прибегают к соответствующим признакам, из которых наиболее часто используют два: признак сравнения и предельный признак.
и тогда для установления сходимости (расходимости) интеграла (7.1) прибегают к соответствующим признакам, из которых наиболее часто используют два: признак сравнения и предельный признак.
Признак сравнения: пусть при 
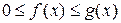 (
(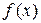 ,
,  – непрерывные функции,
– непрерывные функции,  ). Тогда:
). Тогда:
1) если  – сходится, то
– сходится, то  – сходится;
– сходится;
2) если  – расходится, то
– расходится, то  – расходится.
– расходится.
Предельный признак: пусть при 
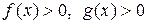 и существует предел
и существует предел  . Тогда интегралы
. Тогда интегралы  ,
,  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
При установлении вопроса о сходимости, расходимости интеграла (7.1) пользуются вспомогательными интегралами вида
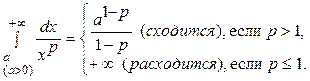 (7.2)
(7.2)
Покажем на примерах, как пользуясь признаками сходимости, расходимости, а также интегралами вида (7.2), установить сходимость или расходимость интеграла (7.1).
Пример 7.1. Показать, что интеграл  – сходится.
– сходится.
Решение: Воспользуемся признаком сравнения: при 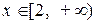
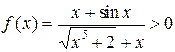 . Задача состоит в том, чтобы подобрать функцию
. Задача состоит в том, чтобы подобрать функцию  такую, чтобы выполнялись одно из условий 1) или 2) признака сравнения.
такую, чтобы выполнялись одно из условий 1) или 2) признака сравнения.
При 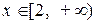 имеем цепочки неравенств:
имеем цепочки неравенств:  ,
, 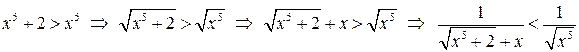 ,
,
 .
.
Итак, в качестве функции  достаточно взять
достаточно взять 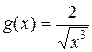 и тогда при
и тогда при 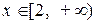
 ,
,  сходится (
сходится (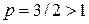 ). Тогда по признаку сравнения интеграл
). Тогда по признаку сравнения интеграл  – сходится.
– сходится.
Пример 7.2 Показать, что интеграл  – расходится.
– расходится.
Решение: Как и в примере 7.1 при 
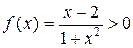 . При
. При  имеем цепочки неравенств:
имеем цепочки неравенств:  (проверьте!),
(проверьте!), 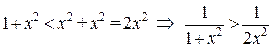 ,
, 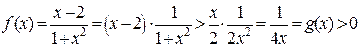 .
.
Здесь в качестве функции  достаточно взять
достаточно взять  и тогда при
и тогда при 
 ,
,  расходится (
расходится (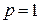 ). Тогда по признаку сравнения исходный интеграл
). Тогда по признаку сравнения исходный интеграл  – расходится.
– расходится.
Если подынтегральная функция 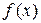 интеграла (7.1) имеет вид дробной функции
интеграла (7.1) имеет вид дробной функции 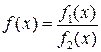 , где
, где 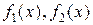 содержат переменную
содержат переменную  в каких-то степенях (в том числе и дробных), то удобно пользоваться предельным признаком сходимости интегралов.
в каких-то степенях (в том числе и дробных), то удобно пользоваться предельным признаком сходимости интегралов.
Пример 7.3. Исследовать на сходимость 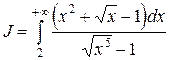 .
.
Решение: Воспользуемся предельным признаком сходимости. Здесь 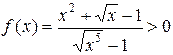 при
при 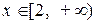 . Задача – найти функцию
. Задача – найти функцию 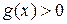 и
и  . Функция
. Функция  отыскивается следующим образом: в числителе и знаменателе функции
отыскивается следующим образом: в числителе и знаменателе функции 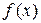 отыскиваются слагаемые, содержащие
отыскиваются слагаемые, содержащие  в старших степенях (старшие степени
в старших степенях (старшие степени  обозначаются соответственно
обозначаются соответственно 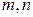 ). В данном случае в числителе – это
). В данном случае в числителе – это  (
( ), а в знаменателе –
), а в знаменателе –  (
(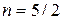 ). Составляется число
). Составляется число  . Тогда в качестве функции
. Тогда в качестве функции  достаточно взять
достаточно взять  (напомним, что
(напомним, что 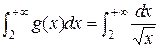 – расходится как интеграл вида (7.2) при
– расходится как интеграл вида (7.2) при 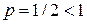 ).
).
Найдем 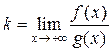 =
= 

 . Итак, по предельному признаку сходимости интеграл
. Итак, по предельному признаку сходимости интеграл  расходится.
расходится.
Дата добавления: 2015-10-30; просмотров: 129 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Численные методы вычисления определенного интеграла | | | Тема ВАЛОВОЙ РЕГИОНАЛЬНЫЙ ПРОДУКТ |