Численные методы вычисления определенного интеграла

Если функция 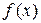такая, что для нее нельзя найти первообразную функцию , а значит, невозможно применить формулу Ньютона-Лейбница для расчета определенного интеграла , часто пользуются численными (приближенными) методами. Рассмотрим следующие методы: формула прямоугольника, формула трапеции, формула параболы (Симпсона).

Формула прямоугольников. Отрезок интегрирования разбивают на равных частей точками

, (), (5.1)

где – шаг (расстояние между двумя соседними точками (5.1) (назовем их узлами)). Тогда формула прямоугольников имеет вид

, (5.2)

где – значения функции 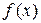в узлах (5.1).

Формула трапеций. Отрезок интегрирования разбивают на равных частей точками (11.1), где . Тогда формула трапеций имеет вид

, (5.3)

где – значения функции 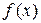в узлах.

Формула парабол (Симпсона). Отрезок интегрирования разбивают на равных частей точками (узлами)

, (), (5.4)

где . Тогда формула парабол (Симпсона) имеет вид

(5.5)

где – значения функции 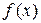в узлах (5.4).

Абсолютная и относительная (в процентах) погрешности методов прямоугольников, трапеций и парабол в случае, если удалось найти точное значение интеграла, имеют вид

. (5.6)

Пример. Вычислить точное и приближенное по методам прямоугольников, трапеций и парабол значения определенного интеграла , разбив отрезок интегрирования на =10 равных частей. Найти абсолютную и относительную погрешности формулы трапеций.

Решение: 1). Вычислим сначала точное значение интеграла:

2). Применим формулу прямоугольников (5.2). В нашем случае , , =10, , . Узлы определяем по формуле (5.1): . Для дальнейших вычислений удобно составить таблицу 5.1 значений , (при вычислении значений берем 4 цифры после запятой).

Таблица 5.1.

i		=	i		=
		0,0000			13,0767
	0,5	1,6956		3,5	15,8469
		3,6056			18,7617
	1,5	5,7119		4,5	12,8146
		8,0000			25,0000
	2,5	10,4583

Теперь формула (5.2) для нашей задачи примет вид

=0,5(1,6956 + 3,6056 + 5,7119 + 8,0000 + 10,4583 + 13,0767 + 15,8469 +

+ 18,7617 + 12,8146 + 25,0000) = 61,98565.

Итак, =55,666, Вычисляем погрешности по формулам (5.6):

3). Применим формулу трапеций (5.3), используя полученную таблицу 5.1 (так как узлы те же самые, что и при использовании метода прямоугольников). Итак, формула трапеций (5.3) для нашей задачи примет вид

= 0,25(0 + 25) + 0,5(1,6956 + 3,6056 + 5,7119 + 8,0000 + 10,4583 + 13,0767 + +15,8469 + 18,7617 + 12,8146) = 6,25 + 0,5 98,9713 = 55,7357.

Итак, =55,666, Вычисляем погрешности по формулам (5.6):

4). Применим формулу парабол (5.5). Имеем , , =10, , . Узлы определяем по формуле (5.4): . Составим таблицу 5.2 значений , (при вычислении значений берем 4 цифры после запятой).

Таблица 5.2.

i		=	i		=
		0,0000		2,75	11,7480
	0,25	0,8197			13,0767
	0,5	1,6956		3,25	14,4433
	0,75	2,6250		3,5	15,8469
		3,6055		3,75	17,2867
	1,25	4,6351			18,7617
	1,5	5,7118		4,25	20,2712
	1,75	6,8339		4,5	12,8146
		8,0000		4,75	23,3910
	2,25	9,2085			25,0000
	2,5	10,45835

Применяя формулу парабол (5.5), получим

= (0,0000 + 25,0000) + 4(0,8197 + 2,6250 + 4,6351 + …. + 23,3910) +

+ (1,6956 + 3,6055 + 5,7118 + … + 12,8146) = 55,6451.

Вычисляем погрешности по формулам (5.6):

Как видно, расчеты по формуле парабол (Симпсона) дают самый точный ответ (самая малая относительная погрешность).

Лекция 4

Дата добавления: 2015-10-30