Метод интегрирования по частям в определенном интеграле

Рассмотренные выше для вычисления неопределенного интеграла метод замены переменной (подстановка и подведение под знак дифференциала) и метод интегрирования по частям также применяются и для вычисления определенного интеграла.

Теорема 1. Пусть выполняются условия:

1) функция интегрируема на отрезке ;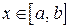

2) функция определена и непрерывна вместе со своей первой производной на отрезке ;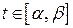

3) – множество значений функции ;

4) , .

Тогда справедлива формула .

Доказательство. Согласно условиям теоремы сложная функция 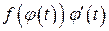непрерывна на отрезке 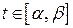. Тогда на отрезке 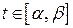для этой функции существует первообразная 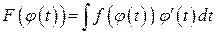. Применяя формулу (9.2), получим

.

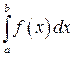Рассмотрим метод подстановки в определенном интеграле. Схема вычисления выглядит здесь следующим образом:

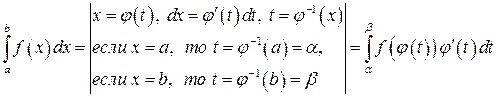, (4.1)

где интеграл справа может оказаться проще исходного интеграла (или вообще, является табличным интегралом). Рассмотрим пример.

Пример 1. Вычислить определенный интеграл .

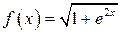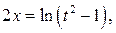Решение. В данном случае функция является непрерывной на отрезке . Воспользуемся формулой (4.1). Примем сначала и отсюда найдем функцию . Имеем для этого или 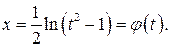Далее имеем .

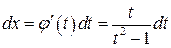Теперь необходимо сделать замену пределов (найти значения ):

если , то ,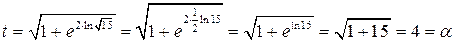

если , то .

Применяя формулу (4.1), получим

.

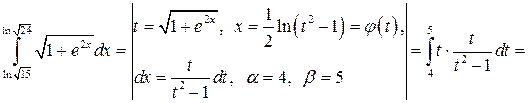
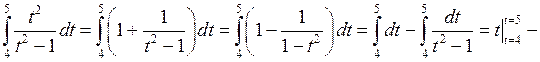
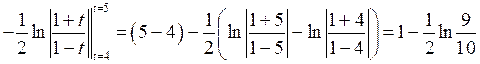Рассмотрим метод подведения функции под знак дифференциала в определенном интеграле. Схема вычисления выглядит здесь следующим образом:

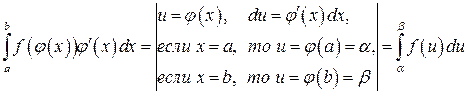, (4.2)

где полученный интеграл справа вычисляется проще, чем исходный интеграл, или вообще сводится к одному из табличных интегралов. Рассмотрим пример.

Пример 2. Вычислить определенные интегралы:

1) ; 2) .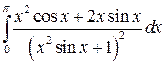

Решение. 1) Подынтегральная функция 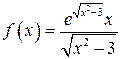является непрерывной на отрезке 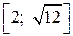. Примем , так как

.

Воспользуемся формулой (4.2):

.

2) Функция 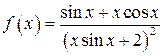является непрерывной на отрезке . Пусть , 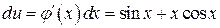. Применение формулы (4.2) дает:

.

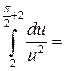
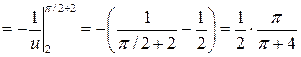Теорема 2. Если функци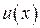и и определены и непрерывны на отрезке вместе со своими производными, тогда справедлива формула

или 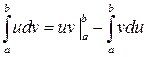. (4.3)

Заметим, что все, что касалось формулы интегрирования по частям в неопределенном интеграле (в том числе и типы интегралов), полностью переносится и на определенный интеграл.

Пример 3. Вычислить определенный интеграл .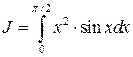

Решение. Вычисляем интеграл по формуле (4.3):

.

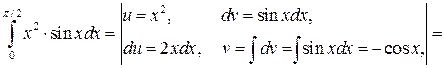
Вычисляем отдельно интеграл 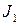по формуле (4.3):

.

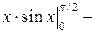
Окончательно .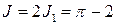

Лекция 3

Дата добавления: 2015-10-30